题目内容
如图，已知：点O在射线AB上，点E在直线上MN上，EA∥OP交AB于A点，∠1=∠3，∠2=∠4．求证：∠A+∠2+∠0EA=180°．分析：根据两直线平行，内错角相等可得∠A=∠1，∠EOP=∠OEA，然后根据平角等于180°可得∠1+∠2+∠EOP=180°，再进行等量代换即可得证．
解答：证明：∵EA∥OP，
∴∠A=∠1，∠EOP=∠OEA，
∴∠1+∠2+∠EOP=180°，
∵∠1=∠3，∠2=∠4，
∴∠A+∠2+∠0EA=180°．
∴∠A=∠1，∠EOP=∠OEA，
∴∠1+∠2+∠EOP=180°，
∵∠1=∠3，∠2=∠4，
∴∠A+∠2+∠0EA=180°．
点评：本题考查了平行线的性质，平角等于180°，熟练掌握性质是解题的关键．
练习册系列答案
相关题目
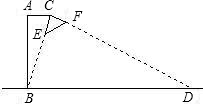如图所示为某种型号的台灯的横截面图，已知台灯灯柱AB长30cm，且与水平桌面垂直，灯臂AC长为15cm，灯头的横截面△CEF为直角三角形，当灯臂AC与灯柱AB垂直时，沿CE边射出的光线刚好射到底座B点，若不考虑其它因素，该台灯在桌面可照亮的宽度BD的长为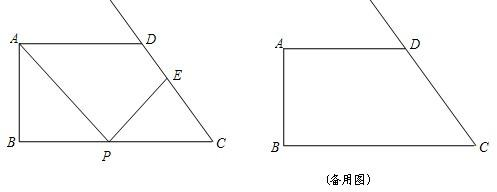
，求A点横坐标的数值.
．点P在边BC上运动（点P不与点B、点C重合），一束光线从点A出发，沿AP的方向射出，经BC反射后，反射光线PE交射线CD于点E．