Question

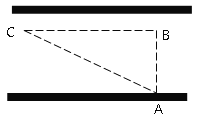
【题目】如图，Ｄ、Ｅ分别是△ＡＢＣ的边ＢＣ、ＡＢ上的点，△ＡＢＣ，△ＢＤＥ，△ＡＣＤ的周长依次为， ， ．

（１）当∠２＝∠３，ＢＤ＝ＢＣ时，求的值；

（２）当∠１＝∠２，ＢＤ＝ＢＣ时，求的值；

（３）当∠１＝∠２＝∠３时，证明： ≤．

Answer 1

【答案】（１）＝；

（２）＝；

（３）证明见解析

【解析】【试题分析】（1）根据相似三角形的周长比等于相似比，即先证明两个三角形相似，

△ＢＤＥ∽△ＢＣＡ，得＝；

（2）∠１＝∠２，∠Ｃ是公共角，得△ＡＣＤ∽△ＢＣＡ，

由＝＝ 得＝＝，由ＢＤ＝ＢＣ，得ＤＣ＝ＢＣ，则＝；

（３）先证明△ＡＣＤ∽△ＢＤＥ∽△ＢＣＡ．

根据相似三角形的性质得： ＝ ①＝＝②

由②得， ＝＝＝＝１－＝１－，

∴＝１－．

＝＋＝１－＋＝－＋＋１＝－，

∵－≤０，∴≤．

【试题解析】

（１）∵∠２＝∠３，∴ＤＥ∥ＡＣ，

∴△ＢＤＥ∽△ＢＣＡ

∴＝，

由ＢＤ＝ＢＣ，得＝，

即＝；

（２）∵∠１＝∠２，∠Ｃ是公共角，

∴△ＡＣＤ∽△ＢＣＡ，

∴＝＝

∴＝＝，

由ＢＤ＝ＢＣ，得ＤＣ＝ＢＣ，

∴＝；

（３）证法一：由∠２＝∠３，得ＤＥ∥ＡＣ，

∴△ＢＤＥ∽△ＢＣＡ；

∠１＝∠２，∠Ｃ是公共角，∴△ＡＣＤ∽△ＢＣＡ，

∴△ＡＣＤ∽△ＢＤＥ∽△ＢＣＡ．

∴＝　　　　　　　　　　 ①

＝＝　　　　　　　　②

由②得， ＝＝

＝＝１－＝１－，

∴＝１－．

＝＋＝１－＋

＝－＋＋１＝－，

∵－≤０，

∴≤．

证法二：由∠２＝∠３，得ＡＣ∥ＤＥ，∴△ＢＣＡ∽△ＢＤＥ．

∵∠１＝∠２，∠Ｃ是公共角，∴△ＢＣＡ∽△ＡＣＤ，

∴△ＢＣＡ∽△ＢＤＥ∽△ＡＣＤ．

∵△ＡＢＣ，△ＥＢＤ，△ＡＤＣ的周长为， ， ，

∴相似比为︰︰，

∴ＢＣ︰ＢＤ︰ＡＣ＝︰︰．

设＝＝＝，

则ＢＣ＝，ＢＤ＝，ＡＣ＝．

ＣＤ＝ＢＣ－ＢＤ＝（），由，得，

等式左边的分子、分母同除以，

得，

设， ，

则，１－＝， ＝１－，

＝＋＝＋＝＋１－

＝－＋＋１＝－，

当＝时， 取得最大值，∴≤．

证法三：证明：由∠２＝∠３，得ＤＥ∥ＡＣ，

∴△ＥＢＤ∽△ＡＢＣ．设相似比为，由题意知，

０＜＜１．则＝＝＝＝．

∵∠２＝∠１，∠Ｃ是公共角，∴△ＤＡＣ∽△ＡＢＣ，

∴＝＝＝．

在△ＡＢＣ中，设ＡＢ＝，ＡＣ＝，ＢＣ＝，

由＝，得ＢＤ＝ＢＣ＝ ，ＣＤ＝ＢＣ－ＢＤ＝－ ．

由＝，得ＤＥ＝ＡＣ＝ ．

由△ＡＢＣ∽△ＤＡＣ，得＝，

得，∴．

∵０＜＜１，∴１－＞０，∴＝ ．

∴＝＋＝＋

＝＝＝＋．

设＝，

则１－＝， ＝１－，

∴＝１－＋＝－＋＋１

＝－，

当＝时， 取得最大值，

∴≤．