题目内容
直径为1的球内放一个正方体，那么这个正方体的棱长的最大值为________．
分析：利用球与其内接正方体的关系，得出球的半径与其内接正方体边长之间的关系是解决本题的关键，发现球的直径就是其内接正方体的体对角线长．
解答：
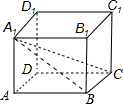解：设这个正方体的棱长的最大值为x，∴A1B=
x=
x，∴这个正方体的体对角线A1C=
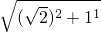x=
x，∵球的直径为1，
∴
x=1，∴x=
．故答案为：
．点评：本题考查空间几何体的内外接问题，要找准球与其内接正方体之间的联系，建立球的半径与正方体边长之间的关系，体现了转化与化归思想．
练习册系列答案
相关题目
19、工人师傅为了检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图1所示的工件槽，其中工件槽的两个底角均为90°，尺寸如图（单位：cm）．将形状规则的铁球放入槽内时，若同时具有图1所示的A，B，E三个接触点，该球的大小就符合要求．图2是过球心O及A，B，E三个接触点的截面示意图．已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切⊙O于点E，AC⊥CD，BD⊥CD．请你结合图1中的数据，计算这种铁球的直径．
AB是⊙O的弦，CD切⊙O于点E，AC⊥CD，BD⊥CD．请你结合图1中的数据，计算这种铁球的直径．
