题目内容
高致病性禽流感是比SARS传染速度更快的传染病.为防止禽流感蔓延,政府规定:离疫点3km范围内为扑杀区;离疫点3km~5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感 病区,如图,在扑杀区内公路CD长为4km.
病区,如图,在扑杀区内公路CD长为4km.
(1)请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);
(2)求这条公路在免疫区内有多少千米?
解:(1)

(2)如图

连接OA、OC,过点O作OE⊥AB于点E,
∴CE= CD=2km,AE=
CD=2km,AE= AB,
AB,
在Rt△OCE中,OE= =
= =
= km,
km,
在Rt△OAE中,AE= =
= =2
=2 km,
km,
∴AB=2AE=4 km,
km,
因此AC+BD=AB-CD=4 -4(km).
-4(km).
答:这条公路在免疫区内有(4 -4)千米.
-4)千米.
分析:(1)在内圆(或外圆)任意作出两条弦,分别作出者两条弦的垂直平分线,它们的交点就是疫点(即圆心O);
(2)利用垂径定理求出AB、CD的长度,问题解决.
点评:此题运用线段的垂直平分线的性质作图及勾股定理解答.

(2)如图

连接OA、OC,过点O作OE⊥AB于点E,
∴CE=
 CD=2km,AE=
CD=2km,AE= AB,
AB,在Rt△OCE中,OE=
 =
= =
= km,
km,在Rt△OAE中,AE=
 =
= =2
=2 km,
km,∴AB=2AE=4
 km,
km,因此AC+BD=AB-CD=4
 -4(km).
-4(km).答:这条公路在免疫区内有(4
 -4)千米.
-4)千米.分析:(1)在内圆(或外圆)任意作出两条弦,分别作出者两条弦的垂直平分线,它们的交点就是疫点(即圆心O);
(2)利用垂径定理求出AB、CD的长度,问题解决.
点评:此题运用线段的垂直平分线的性质作图及勾股定理解答.

练习册系列答案
相关题目
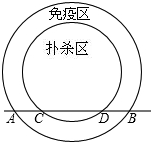 病区,如图,在扑杀区内公路CD长为4km.
病区,如图,在扑杀区内公路CD长为4km. 高致病性禽流感是比SARS病毒传染速度更快的传染病.
高致病性禽流感是比SARS病毒传染速度更快的传染病. 个提醒标志牌,问如有一辆汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区?
个提醒标志牌,问如有一辆汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区?
