题目内容
如图，已知抛物线
，与
轴交于A、B两点，点
为抛物线的顶点。点P在抛物线的对称轴上，设⊙P的半径为
，当⊙P与轴和直线BC都相切时，则圆心P的坐标为 ． 
，与轴交于A、B两点，点为抛物线的顶点。点P在抛物线的对称轴上，设⊙P的半径为，当⊙P与轴和直线BC都相切时，则圆心P的坐标为 ． 
，
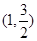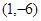
解：设P点坐标为（1，a），
∵抛物线的解析式为
∴抛物线顶点C的坐标为（1，4），
令y=0，解得B点的坐标为（4，0），
设直线BC的解析式为y=kx+b，
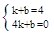
解得k=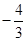
，b=
，
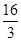则直线BC的解析式为y=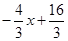
点P到直线BC的距离d=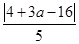
点P到x轴的距离为|a|，
又知⊙P与x轴和直线BC都相切时，
即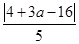=|a|
解得a=
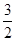或a=-6
故P点的坐标为(1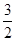，)或（1，-6）．
∵抛物线的解析式为
∴抛物线顶点C的坐标为（1，4），
令y=0，解得B点的坐标为（4，0），
设直线BC的解析式为y=kx+b，
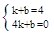
解得k=
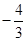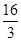，b=，则直线BC的解析式为y=
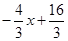
点P到直线BC的距离d=
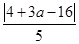
点P到x轴的距离为|a|，
又知⊙P与x轴和直线BC都相切时，
即
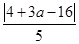=|a|解得a=
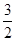或a=-6故P点的坐标为(1，
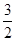)或（1，-6）．
练习册系列答案
名校课堂系列答案
相关题目
的对称轴为直线_______，顶点坐标为______，与
轴的交点坐标为________；
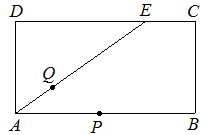
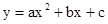与x轴正半轴交于A、B两点，与y轴交于点C，直线
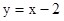经过A、C两点，且AB=2.
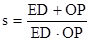，当t 为何值时，s有最小值，并求出最小值。
上两点，则抛物线的对称轴是（ ）
，当
时，它是二次函数.
恒成立，那么实数x的取值范围是