题目内容
(2012•河源)一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一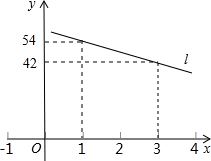 次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
(1)求直线l的函数关系式;
(2)如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是多少?
 次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.(1)求直线l的函数关系式;
(2)如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是多少?
分析:(1)根据直线l的解析式是y=kx+b,将(3,42),(1,54)代入求出即可;
(2)利用y=-6x+60≥10,求出x的取值范围,进而得出警车行驶的最远距离.
(2)利用y=-6x+60≥10,求出x的取值范围,进而得出警车行驶的最远距离.
解答:解:(1)设直线l的解析式是y=kx+b,由题意得
,
解得
,
故直线l的解析式是:y=-6x+60;
(2)由题意得:y=-6x+60≥10,
解得x≤
,
故警车最远的距离可以到:60×
×
=250千米.
|
解得
|
故直线l的解析式是:y=-6x+60;
(2)由题意得:y=-6x+60≥10,
解得x≤
| 25 |
| 3 |
故警车最远的距离可以到:60×
| 25 |
| 3 |
| 1 |
| 2 |
点评:此题主要考查了待定系数法求一次函数解析式和不等式解法,利用数形结合得出函数解析式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•河源)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )
(2012•河源)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )
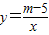 (m为常数)图象的一支.
(m为常数)图象的一支.
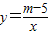 (m为常数)图象的一支.
(m为常数)图象的一支.