题目内容
 如图,四边形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函数
如图,四边形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函数 的图象经过对角线BD的中点M,与BC,CD的边分别交于点P、Q.
的图象经过对角线BD的中点M,与BC,CD的边分别交于点P、Q.
(1)直接写出点M,C的坐标;
(2)求直线BD的解析式;
(3)线段PQ与BD是否平行?并说明理由.
解:(1)∵点M是线段B、D的中点,B(3,1),D(1,3),
∴点M的横坐标为: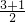 =2,点M的纵坐标为:
=2,点M的纵坐标为: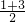 =2,
=2,
∴点M的坐标为(2,2),
∵四边形ABCD是正方形,
∴点B与点C的横坐标相同,点C与点D的纵坐标相同即可求出C点坐标;
∴点C的坐标为(3,3);
(2)设直线BD的解析式为y=kx+b,
∵B(3,1),D(1,3)在直线BD上,
∴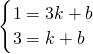 ,解得
,解得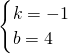 .
.
∴直线BD的解析式为y=-x+4;
(3)PQ∥BD.理由如下:
∵反比例函数 的图象经过M(2,2),
的图象经过M(2,2),
∴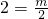 ,解得m=4.
,解得m=4.
∴反比例函数的解析式为 .
.
∵反比例函数 的图象与BC交于点P,
的图象与BC交于点P,
∴点P的横坐标为3,当x=3时,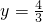 .
.
∴点P的坐标为(3, ).
).
同理点Q的坐标为( ,3).
,3).
∴CP=CQ= .
.
∴∠CPQ=45°.
又∵∠CBD=45°,
∴∠CPQ=∠CBD.
∴PQ∥BD.
分析:(1)直接根据中点坐标公式即可求出点M的坐标;再根据点B与点C的横坐标相同,点C与点D的纵坐标相同即可求出C点坐标;
(2)设直线BD的解析式为y=kx+b,由已知B(3,1),D(1,3),再把B、D两点的坐标代入即可求出k、b的值,进而得出结论;
(3)先根据反比例函数y= 过点M(2,2)可求出m的值,由此可求出点P、Q两点的坐标,故可得出CP=CQ=
过点M(2,2)可求出m的值,由此可求出点P、Q两点的坐标,故可得出CP=CQ= ,即∠CPQ=45°,再由直线BD是正方形ABCD的对角线可知∠CBD=45°,故∠CPQ=∠CBD,进而可得出结论.
,即∠CPQ=45°,再由直线BD是正方形ABCD的对角线可知∠CBD=45°,故∠CPQ=∠CBD,进而可得出结论.
点评:本题考查的是反比例函数综合题,涉及到正方形的性质、用待定系数法求一次函数及反比例函数的解析式等知识,难度适中.
∴点M的横坐标为:
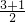 =2,点M的纵坐标为:
=2,点M的纵坐标为: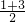 =2,
=2,∴点M的坐标为(2,2),
∵四边形ABCD是正方形,
∴点B与点C的横坐标相同,点C与点D的纵坐标相同即可求出C点坐标;
∴点C的坐标为(3,3);
(2)设直线BD的解析式为y=kx+b,
∵B(3,1),D(1,3)在直线BD上,
∴
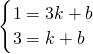 ,解得
,解得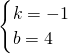 .
.∴直线BD的解析式为y=-x+4;
(3)PQ∥BD.理由如下:
∵反比例函数
 的图象经过M(2,2),
的图象经过M(2,2),∴
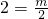 ,解得m=4.
,解得m=4.∴反比例函数的解析式为
 .
.∵反比例函数
 的图象与BC交于点P,
的图象与BC交于点P,∴点P的横坐标为3,当x=3时,
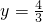 .
.∴点P的坐标为(3,
 ).
).同理点Q的坐标为(
 ,3).
,3).∴CP=CQ=
 .
.∴∠CPQ=45°.
又∵∠CBD=45°,
∴∠CPQ=∠CBD.
∴PQ∥BD.
分析:(1)直接根据中点坐标公式即可求出点M的坐标;再根据点B与点C的横坐标相同,点C与点D的纵坐标相同即可求出C点坐标;
(2)设直线BD的解析式为y=kx+b,由已知B(3,1),D(1,3),再把B、D两点的坐标代入即可求出k、b的值,进而得出结论;
(3)先根据反比例函数y=
 过点M(2,2)可求出m的值,由此可求出点P、Q两点的坐标,故可得出CP=CQ=
过点M(2,2)可求出m的值,由此可求出点P、Q两点的坐标,故可得出CP=CQ= ,即∠CPQ=45°,再由直线BD是正方形ABCD的对角线可知∠CBD=45°,故∠CPQ=∠CBD,进而可得出结论.
,即∠CPQ=45°,再由直线BD是正方形ABCD的对角线可知∠CBD=45°,故∠CPQ=∠CBD,进而可得出结论.点评:本题考查的是反比例函数综合题,涉及到正方形的性质、用待定系数法求一次函数及反比例函数的解析式等知识,难度适中.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.