题目内容
对于抛物线 
.
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
| x | … | | | | | | … |
| y | … | | | | | | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程
（t为实数）在
＜x＜
的范围内有解，则t的取值范围是 ．
（1）它与x轴交点的坐标为：（-1，0）（-3，0），与y轴交点的坐标为（0，3），顶点坐标为（2，-1）；故答案为：（1，0）（3，0），（0，3）（2，-1）
（2）列表：
图象如图所示．x … 0 1 2 3 4 … y … 3 0 -1 0 3 … 
（3）∵关于x的一元二次方程x2-4x+3-t=0（t为实数）在-1＜x＜
的范围内有解，
∵y=x2-4x+3的顶点坐标为（2，-1），
若x2-4x+3-t=0有解，方程有两个根，则：b2-4ac=16-4（3-t）≥0，
解得：-1≤t
当x=-1，代入x2-4x+3-t=0，t=8，
∵x＞-1，∴t＜8，
∴t的取值范围是：-1≤t＜8，
故填：-1≤t＜8
解析
练习册系列答案
天天练口算系列答案
相关题目
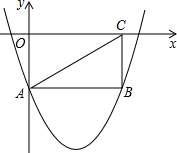如图，矩形OABC的两边在坐标轴上，且A（0，-2），AB=4，连接AC，抛物线y=x2+bx+c经过A，B两点．点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动．