Question

【题目】数学活动：探究与发现

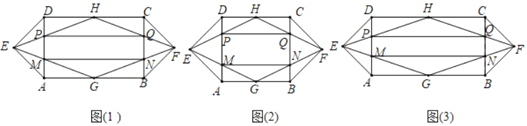
定义：如图(1)，四边形ABCD为矩形，△ADE和△BCF均为等腰直角三角形，∠AED＝∠BFC＝90°，点G、H分别为AB、CD的中点，连接EG、EH、FG、FH，分别与AD、BC交于点M、P、N、Q，我们把四边形PQNM叫做矩形ABCD的递推四边形．

独立思考：

(1)求证：四边形PQNM矩形．

合作交流：

(2)解决完上述问题后，“兴趣”小组的同学们对正方形ABCD的递推四边形进行了探究，如图(2)，他们猜想矩形PQNM的宽与长的比．他们猜想的结论是否正确？请说明理由．

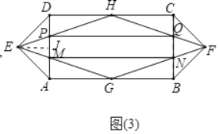
发现问题：(3)在“兴趣”小组同学们的启发下，“实践”小组的同学们对宽与长的比为的矩形的递推四边形进行了探究，如图(3)．他们提出如下问题：

①在矩形ABCD中，若，则矩形PQNM的宽与长的比为_____；

②在矩形ABCD中，若，则矩形PQNM的宽与长的比为______；

③在矩形ABCD中，若，则矩形PQNM的宽与长的比为______．

任务：请你完成“实践”小组提出的数学问题．(注：直接写出结果，不要求说理或证明)

Answer 1

【答案】(1)证明见解析；(2)猜想正确，证明见解析；(3)①1：6；②1：12；③1：n(n+1)．

【解析】

（1）根据矩形的判定方法进行证明即可；

（2）如图2中，作EJ⊥AD于J．设正方形的边长为2a．则DH＝HC＝a，继而求出PM、PQ即可解决问题；

（3）①如图3中，作EJ⊥AD于J．设AD＝m，DC＝2m，根据等腰直角三角形的性质，平分线分线段成比例的性质，求出PM、PQ即可得；

②作EJ⊥AD于J．设AD＝m，DC＝3m，求出PM、OQ即可解决问题；

③根据①②探究规律，利用规律解决问题即可.

(1)如图1中，

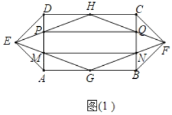
∵四边形ABCD是矩形，

∴∠ADC＝∠BCD＝90°，AD＝BC，AD∥BC，

∵∠AED＝∠BFC＝90°，ED＝EA，FC＝FB，

∴∠ADE＝∠EAD＝∠FCB＝∠FBC＝45°，

∴△ADE≌△BFC(ASA)，∠EDH＝∠FCH＝135°

∴DE＝FC，

∵DH＝CH，

∴△EDH≌△FCH(SAS)，

∴∠DHE＝∠FHC，

∵∠PDH＝∠QCH＝90°，

∴△HDP≌△HCQ(ASA)，

∴DP＝CQ，∵DP∥CQ，

∴四边形DPQC是平行四边形，

∵∠PDC＝90°，

∴四边形DPQC是矩形，

∴∠DPQ＝∠CQP＝90°，

∴∠MPQ＝∠NQP＝90°，

同法可证：∠PMN＝∠QNM＝90°，

∴四边形PMNQ是矩形．

(2)结论：猜想正确．

理由：如图2中，作EJ⊥AD于J．设正方形的边长为2a．则DH＝HC＝a．

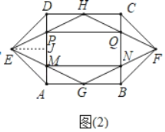
∵ED＝EA，∠AED＝90°，EJ⊥AD，

∴AJ＝DJ＝a，

∴EJ＝AJ＝DJ＝a，

∵∠EJP＝∠HDP＝90°，∠DPH＝∠EPJ，DH＝EJ＝a，

∴△DPH≌△JPE(AAS)，

∴DP＝PJ，

易证DP＝AM，

∴DP＝PJ＝JM＝AM，

∴PM＝a，

∵PQ＝CD＝2a，

∴＝．

(3)①如图3中，作EJ⊥AD于J．设AD＝m，DC＝2m．

易知：EJ＝DJ＝AJ＝m，DH＝CH＝m，

∵DH∥EJ，

∴＝＝2，

可得PJ＝JM＝m，PM＝m，PQ＝CD＝2m，

∴＝＝．

②作EJ⊥AD于J．设AD＝m，DC＝3m．

易知：EJ＝DJ＝AJ＝m，DH＝CH＝1.5m，

∵DH∥EJ，

∴＝＝3，

可得PJ＝JM＝m，PM＝m，PQ＝CD＝3m，

∴＝＝．

③由①②可知：PM：PQ＝1：n(n+1)，

故答案为1：6，1：12，1：n(n+1)．