题目内容
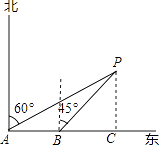
【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1, ![]() ≈1.73)
≈1.73)
【答案】解:过点P作PC⊥AB于C点,即PC的长为轮船与灯塔的最短距离,根据题意,得
AB=18× ![]() =6,∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,∠PCB=90°,
=6,∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,∠PCB=90°,
∴PC=BC,
在Rt△PAC中,tan30°= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得PC=3 ![]() +3≈8.2(海里),
+3≈8.2(海里),
∴轮船与灯塔的最短距离约为8.2海里.
【解析】根据题意,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,得到AB![]() =6,∠PAB=30°,∠PBC=45°,∠PCB=90°,所以PC=BC,在Rt△PAC中,根据三角函数值求出tan3
=6,∠PAB=30°,∠PBC=45°,∠PCB=90°,所以PC=BC,在Rt△PAC中,根据三角函数值求出tan3![]() 0°,
0°,![]() 解得PC≈8.2(海里),所以轮船与灯塔的最短距离约为8.2海里.
解得PC≈8.2(海里),所以轮船与灯塔的最短距离约为8.2海里.
【考点精析】掌握关于方向角问题是解答本题的根本,需要知道指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
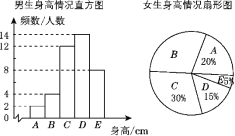
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.