题目内容
 如图,将边长为
如图,将边长为| 6 |
分析:由旋转角∠BAB′=30°,可知∠DAB′=90°-30°=60°;设B′C′和CD的交点是O,连接OA,构造全等三角形,用S阴影部分=S正方形-S四边形AB′OD,计算面积即可.
解答: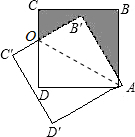 解:设B′C′和CD的交点是O,连接OA,
解:设B′C′和CD的交点是O,连接OA,
∵AD=AB′,AO=AO,∠D=∠B′=90°,
∴Rt△ADO≌Rt△AB′O,
∴∠OAD=∠OAB′=30°,
∴OD=OB′=
,
S四边形AB′OD=2S△AOD=2×
×
=2
,
∴S阴影部分=S正方形-S四边形AB′OD=6-2
.
 解:设B′C′和CD的交点是O,连接OA,
解:设B′C′和CD的交点是O,连接OA,∵AD=AB′,AO=AO,∠D=∠B′=90°,
∴Rt△ADO≌Rt△AB′O,
∴∠OAD=∠OAB′=30°,
∴OD=OB′=
| 2 |
S四边形AB′OD=2S△AOD=2×
| 1 |
| 2 |
| 2 |
| 6 |
| 3 |
∴S阴影部分=S正方形-S四边形AB′OD=6-2
| 3 |
点评:此题的重点是能够计算出四边形的面积.注意发现全等三角形.

练习册系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
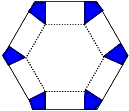 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为