题目内容
 如图,把直角三角形ABC的斜边AB放在定直线L上,按顺时针方向在L上转动两次使它转到三角形A″B″C″的位置,设BC=1,AC=
如图,把直角三角形ABC的斜边AB放在定直线L上,按顺时针方向在L上转动两次使它转到三角形A″B″C″的位置,设BC=1,AC= ,其中∠A=30°则定点A运动到点A″的位置时,点A经过的路线长是________.
,其中∠A=30°则定点A运动到点A″的位置时,点A经过的路线长是________.
 π+
π+
分析:在△ABC中,BC=1,AC=
 ,根据勾股定理得到AB的长为2.求出∠CAB、∠CBA,顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是两个扇形的面积+△A′BC″的面积.根据扇形的面积公式可以进行计算.
,根据勾股定理得到AB的长为2.求出∠CAB、∠CBA,顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是两个扇形的面积+△A′BC″的面积.根据扇形的面积公式可以进行计算.解答:∵在Rt△ACB中,BC=1,AC=
 ,
,∴由勾股定理得:AB=2,
∴AB=2BC,
∴∠CAB=30°,∠CBA=60°,
∴∠ABA′=120°,∠A″C″A′=90°,
S=
 +
+ +
+ ×1×
×1× =
= π+
π+ .
.故答案为:
 π+
π+ .
.点评:本题考查了扇形的面积计算,勾股定理,含30度角的直角三角形的性质的应用,本题的关键是弄清顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的图形的形状.

练习册系列答案
相关题目
 如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=
如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC= 它转到△A″B″C″的位置,设BC=1,AC=
它转到△A″B″C″的位置,设BC=1,AC= 12、如图,把直角三角形ABC绕直角顶点C顺时针方向旋转90°后到达△A1B1C,延长AB交A1B1于D,则∠ADA1=
12、如图,把直角三角形ABC绕直角顶点C顺时针方向旋转90°后到达△A1B1C,延长AB交A1B1于D,则∠ADA1=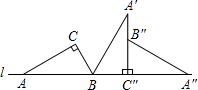 如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2
如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2