题目内容
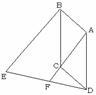
已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F ，使CF＝CE，连结DF，交BE的延长线于点G，连结OG．
（1）求证：△BCE≌△DCF；
（2）OG与BF有什么数量关系？证明你的结论；
（3）若GE·GB＝4－2
，求 正方形ABCD的面积．
（1）求证：△BCE≌△DCF；
（2）OG与BF有什么数量关系？证明你的结论；
（3）若GE·GB＝4－2
，求 正方形ABCD的面积．（1）（2）略 （3）4
（1）（2）略
（3）设BC=x，则DC＝x ,BD＝
，CF＝（－1）x
GD2=GE·GB=4－2 DC2+CF2=(2GD)2 即 x2+（－1）2x2＝4（4－2）
（4－2）x2＝4（4－2） x2＝4 正方形ABCD的面积是4个平方单位
（1）利用正方形的性质，由全等三角形的判定定理SAS即可证得△BCE≌△DCF；
（2）通过△DBG≌△FBG的对应边相等知BD=BF；然后由三角形中位线定理证得OG=
BF
（3）设BC=x，利用勾股定理解x，从而求得正方形ABCD的面积
（3）设BC=x，则DC＝x ,BD＝
，CF＝（－1）xGD2=GE·GB=4－2
DC2+CF2=(2GD)2 即 x2+（－1）2x2＝4（4－2）（4－2
）x2＝4（4－2） x2＝4 正方形ABCD的面积是4个平方单位（1）利用正方形的性质，由全等三角形的判定定理SAS即可证得△BCE≌△DCF；
（2）通过△DBG≌△FBG的对应边相等知BD=BF；然后由三角形中位线定理证得OG=
BF（3）设BC=x，利用勾股定理解x，从而求得正方形ABCD的面积
练习册系列答案
相关题目
，D是边BC上的一点，DE∥CA交AB于点E， DF∥BA交AC于点F. 要使四边形AEDF是菱形，只需添加条件
为矩形
的对角线，则图中
与
一定不相等的是（ ）
A． B． C． D．
中，
，
为
中点，
，
于点
，
∥
，
于点
，交
于点
．
的度数．
），D（6，
），并将各点用线段一次连接构成一个四边形ABCD。