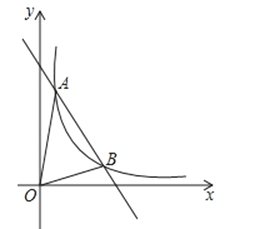
��Ŀ����
����Ŀ����֪������������![]() ��
�� ![]() ����
����![]() ��Ӧ������
��Ӧ������![]() ����
����![]() ��Ӧ������
��Ӧ������![]() ��
��
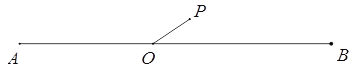
��![]() ����ͼ
����ͼ![]() ������������
������������![]() ��
�� ![]() �ֱ��
�ֱ��![]() ��
�� ![]() ����ͬʱ�����˶�����
����ͬʱ�����˶�����![]() ���ٶ��ǵ�
���ٶ��ǵ�![]() ���ٶ�
���ٶ�![]() ����
����![]() ����λ����/�룬����
����λ����/�룬����![]() �룬��
�룬��![]() �ϵ�
�ϵ�![]() ����
����![]() ���ٶȣ�
���ٶȣ�
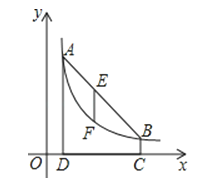
��![]() ����ͼ
����ͼ![]() ��
�� ![]() ��ʾԭ�㣬����
��ʾԭ�㣬����![]() ��
�� ![]() �ֱ��
�ֱ��![]() ��
�� ![]() ����ͬʱ���������˶���ͬʱ����
����ͬʱ���������˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ���������˶�����
���������˶�����![]() ��
�� ![]() ��
�� ![]() ���ٶȷֱ�Ϊ
���ٶȷֱ�Ϊ![]() ����λ����/�롢
����λ����/�롢![]() ����λ����/�롢
����λ����/�롢![]() ����λ����/�룻�����
����λ����/�룻�����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��˵�����˶������е�����ϵ
���е㣬��˵�����˶������е�����ϵ![]() ʼ�ճ�����
ʼ�ճ�����
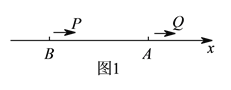
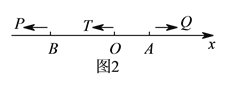
���𰸡���1��16����λ����/�룻��2��֤��������
���������⣺��1�����Q���ٶ�Ϊx����λ����/�룬
���P���ٶ�Ϊ��2x-4������λ����/�룬[40-��-80��]+10x=10��2x-4����
��120+10x=20x-40��
��x=16����λ����/�룮
��2�����˶�ʱ��Ϊt��
��PQ=120+5t+2t=120+7t��OT=t��
��PQ+OT=120+8t��MN=MO+ON=MT+TO+ON=![]() ��5t+80-t��+t+
��5t+80-t��+t+![]() ��40+2t��=4t+60��
��40+2t��=4t+60��
��2MN=8t+120��
��PQ=OT=2MN��

��ϰ��ϵ�д�
�����Ŀ