题目内容
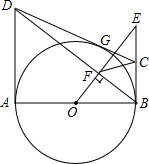 如图,AB为⊙0的直径,DC、DA、CB分别切⊙O于G、A、B,OE⊥BD于F,交BC的延长线于E,连CF.
如图,AB为⊙0的直径,DC、DA、CB分别切⊙O于G、A、B,OE⊥BD于F,交BC的延长线于E,连CF.(1)求证:
| BC |
| OB |
| OA |
| AD |
(2)若tan∠ABD=
| 3 |
| 4 |
考点:切线的性质,相似三角形的判定与性质
专题:
分析:(1)首先连接OC,OD,由DC、DA、CB分别切⊙O于G、A、B,根据切线的性质与切线长定理,可证得∠COD=90°,继而可证得△DOA∽△OCB,然后由相似三角形的对应边成比例,证得结论;
(2)由tan∠ABD=
,可证得CB=
OB,易证得C是BE的中点,继而可得∠CFE=∠CEF=∠ABD,则可证得结论.
(2)由tan∠ABD=
| 3 |
| 4 |
| 2 |
| 3 |
解答: (1)证明:连接OC,OD,
(1)证明:连接OC,OD,
∵DC、DA、CB分别切⊙O于G、A、B,
∴∠A=∠OBC=90°,∠ODA=∠ODG=
∠ADG,∠OCB=∠OCG=
∠BCG,
∵∠ADG+∠BCG=180°,
∴∠ODG+∠OCG=90°,
∴∠COD=90°,
∴∠AOD+∠BOC=90°,
∵∠AOD+∠ODA=90°,
∴∠ODA=∠BOC,
∴△DOA∽△OCB,
∴
=
;
(2)解:∵tan∠ABD=
,
∴
=
,
∵OA=OB=
AB,
∴
=
=
,
∴CB=
OB,
在Rt△OBE中,BF⊥OE,
∴∠BEO=∠ABD,
∴tan∠OEB=tan∠ABD=
,
即
=
,
∴BE=
OB,
∴BC=
BE,
即C是BE的中点,
∵BF⊥FE,
∴CF=CE=
BE,
∴∠CFE=∠CEF=∠ABD,
∴tan∠CFE=tan∠ABD=
.
 (1)证明:连接OC,OD,
(1)证明:连接OC,OD,∵DC、DA、CB分别切⊙O于G、A、B,
∴∠A=∠OBC=90°,∠ODA=∠ODG=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADG+∠BCG=180°,
∴∠ODG+∠OCG=90°,
∴∠COD=90°,
∴∠AOD+∠BOC=90°,
∵∠AOD+∠ODA=90°,
∴∠ODA=∠BOC,
∴△DOA∽△OCB,
∴
| BC |
| OB |
| OA |
| AD |
(2)解:∵tan∠ABD=
| 3 |
| 4 |
∴
| AD |
| AB |
| 3 |
| 4 |
∵OA=OB=
| 1 |
| 2 |
∴
| CB |
| OB |
| OA |
| AD |
| 2 |
| 3 |
∴CB=
| 2 |
| 3 |
在Rt△OBE中,BF⊥OE,
∴∠BEO=∠ABD,
∴tan∠OEB=tan∠ABD=
| 3 |
| 4 |
即
| OB |
| BE |
| 3 |
| 4 |
∴BE=
| 4 |
| 3 |
∴BC=
| 1 |
| 2 |
即C是BE的中点,
∵BF⊥FE,
∴CF=CE=
| 1 |
| 2 |
∴∠CFE=∠CEF=∠ABD,
∴tan∠CFE=tan∠ABD=
| 3 |
| 4 |
点评:此题考查了切线的性质、切线长定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 一个几何体的三视图如图所示,这个几何体是( )
一个几何体的三视图如图所示,这个几何体是( )| A、球体 | B、长方体 |
| C、圆锥体 | D、圆柱体 |
 操作:如图,已知正方形纸片ABCD的边长为10,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,当P刚好位于DP=
操作:如图,已知正方形纸片ABCD的边长为10,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,当P刚好位于DP= 如图,△ABC中,AB=AC,∠BA0=45°,△ABC内接于⊙0,D为⊙O上一点,过点D作⊙O的切线交BC的延长线于E,若DE⊥BC,AD=2
如图,△ABC中,AB=AC,∠BA0=45°,△ABC内接于⊙0,D为⊙O上一点,过点D作⊙O的切线交BC的延长线于E,若DE⊥BC,AD=2
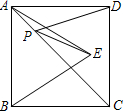 如图.正方形ABCD的面积为9,△ABE是等边三角形,点E在正方形ABCD内,P为对角线AC上一动点,使PD+PE最小,则这个最小值为
如图.正方形ABCD的面积为9,△ABE是等边三角形,点E在正方形ABCD内,P为对角线AC上一动点,使PD+PE最小,则这个最小值为