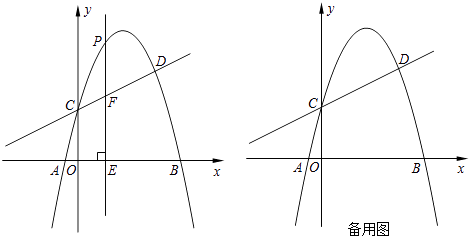题目内容
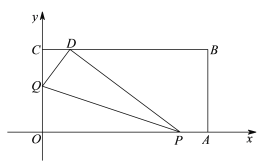
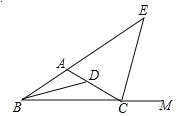
【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s). 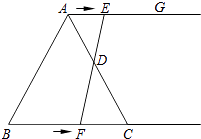
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.
【答案】
(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
∵在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(AAS)
(2)6;1.5
【解析】(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6, 则此时的时间t=6÷1=6(s);
②四边形AFCE为直角梯形时,
(Ⅰ)若CE⊥AG,则AE=CF= ![]() BC=3,BF=3×2=6,即点F与点C重合,不是直角梯形.
BC=3,BF=3×2=6,即点F与点C重合,不是直角梯形.
(Ⅱ)若AF⊥BC,
∵△ABC为等边三角形,
∴F为BC中点,即BF=3,
∴此时的时间为3÷2=1.5(s);
故答案为:6;1.5.
(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;(2)①若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可;②分两种情况考虑:若CE⊥AG,此时四点构成三角形,不是直角梯形;若AF⊥BC,求出BF的长度及时间t的值.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
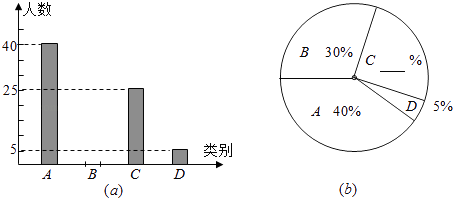
初中学业考试导与练系列答案【题目】从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解”雾霾天气的主要原因“,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: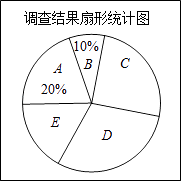
(1)填空:m= , n= . 扇形统计图中E组所占的百分比为%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?