题目内容
7.一次函数y=-4x+12的图象与x轴交点坐标是(3,0),与y轴交点坐标是(0,12),图象与坐标轴所围成的三角形面积是18.分析 根据坐标轴上点的坐标特征求出直线与x轴和y轴的交点坐标,然后根据三角形面积公式计算图象与坐标轴所围成的三角形面积.
解答 解:当y=0时,-4x+12=0,解得x=3,所以直线与x轴交点坐标是(3,0),
当x=0时,y=-4x+12=12,所以直线与y轴交点坐标是(0,12),
所以图象与坐标轴所围成的三角形面积=$\frac{1}{2}$×3×12=18.
故答案为(3,0),(0,12),18.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
17.在求1+6+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
S=1+6+62+63+64+65+66+67+68+69①然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②-①得6S-S=610-1,即5S=610-1,所以S=$\frac{{6}^{10}-1}{5}$,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是( )
S=1+6+62+63+64+65+66+67+68+69①然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②-①得6S-S=610-1,即5S=610-1,所以S=$\frac{{6}^{10}-1}{5}$,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是( )
| A. | $\frac{{a}^{2014}-1}{a-1}$ | B. | $\frac{{a}^{2015}-1}{a-1}$ | C. | $\frac{{a}^{2014}-1}{a}$ | D. | a2014-1 |
19.下列四个选项中,∠1与∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
16. 一机器零件如图,其主视图为( )
一机器零件如图,其主视图为( )
 一机器零件如图,其主视图为( )
一机器零件如图,其主视图为( )| A. |  | B. |  | C. |  | D. |  |
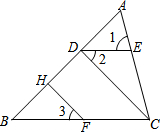 已知,如图,DE∥BC,∠A=60°,∠B=50°;
已知,如图,DE∥BC,∠A=60°,∠B=50°;