题目内容
 如图,直线
如图,直线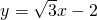 与双曲线
与双曲线 (k>0)在第一象限内的交点为R,与x轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积是4:1,则k等于________.
(k>0)在第一象限内的交点为R,与x轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积是4:1,则k等于________.

分析:先求出Q的坐标为(0,-2),P点坐标为(
 ,0),易证Rt△OQP∽Rt△MRP,根据三角形相似的性质得到
,0),易证Rt△OQP∽Rt△MRP,根据三角形相似的性质得到 =
= =
= ,分别求出PM、RM,得到OM的长,从而确定R点坐标,然后代入
,分别求出PM、RM,得到OM的长,从而确定R点坐标,然后代入 (k>0)求出k的值.
(k>0)求出k的值.解答:对于y=
 x-2,
x-2,令x=0,则y=-2,
∴Q的坐标为(0,-2),即OQ=2;
令y=0,则x=
 ,
,∴P点坐标为(
 ,0),即OP=
,0),即OP= ;
;∵Rt△OQP∽Rt△MRP,
而△OPQ与△PRM的面积是4:1,
∴
 =
= =
= ,
,∴PM=
 OP=
OP= ,RM=
,RM= OQ=1,
OQ=1,∴OM=OP+PM=
 ,
,∴R点的坐标为(
 ,1),
,1),∴k=
 ×1=
×1= .
.故答案为
 .
.点评:本题考查了解反比例函数的综合题.点在函数图象上,点的横纵坐标满足图象的解析式;三角形相似的性质:相似三角形面积的比等于相似比的平方,对应边的比相等.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
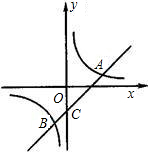 如图,直线与双曲线相交于A(1,2)与B(-2,n).
如图,直线与双曲线相交于A(1,2)与B(-2,n). 已知:如图,直线
已知:如图,直线 与双曲线
与双曲线 与双曲线
与双曲线 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
 直接写出点B的坐标;
直接写出点B的坐标; 经过点B吗?请说明理由.
经过点B吗?请说明理由. 与双曲线
与双曲线 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
 直接写出点B的坐标;
直接写出点B的坐标; 经过点B吗?请说明理由
经过点B吗?请说明理由