题目内容
【题目】如图，正方形ABCO的边长为4，点E在线段AB上运动，AE=BF，且AF与OE相交于点P，直线y=
x-3与x轴，y轴交于M、N两点，连接PN，PM，则△PMN面积的最大值（ ）
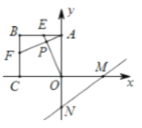
A. 10.5 B. 12 C. 12.5 D. 15
【答案】D
【解析】
证明
≌
，得到
即可可以说明点P在以AO为直径的圆上，要求△PMN面积的最大值，只要求出点P到直线
的最大距离即可.
由题意易得≌ 
四边形ABCO是正方形
点P在以AO为直径的圆上
要使得△PMN的面积最大，点P到直线的距离最大，即平移直线MN使其与圆相切于点P使，距离最大，则过点P做直线MN的垂线与MN交于点H，此时PH一定过圆心G，如图所示：
当
时，
得
，
当
时，得
，
在
中，有
△PMN的最大面积
.
故选：D.
练习册系列答案
相关题目
