题目内容
 如图,点P的坐标为(2,
如图,点P的坐标为(2, ),过点P作x轴的平行线交y轴于点A,交双曲线
),过点P作x轴的平行线交y轴于点A,交双曲线 (x>0)于点N,作PM⊥AN交双曲线
(x>0)于点N,作PM⊥AN交双曲线 (x>0)于点M,连接AM.已知PN=4.
(x>0)于点M,连接AM.已知PN=4.
(1)求k的值.
(2)求△APM的周长.
解:(1)∵点P的坐标为 ,可得AP=2,
,可得AP=2, .
.
又∵PN=4,∴可得AN=6,
∴点N的坐标为 .
.
把 代入
代入 中,得k=9.
中,得k=9.
(2)∵k=9,∴双曲线方程为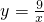 .
.
当x=2时, .∴
.∴ .
.
又∵PM⊥AN,
∴AM= =
=
∴C△APM=5+ .
.
分析:(1)寻找经过双曲线 的点的坐标,由P点的坐标入手,可求的N点的坐标,代入即可得出K的值.
的点的坐标,由P点的坐标入手,可求的N点的坐标,代入即可得出K的值.
(2)求△APM的周长,先求出各个边的长度,AP的长度为P点的横坐标已知,MP的长度为M的纵坐标减去P的纵坐标,再利用勾股定理求出AM即可.
点评:本题通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.
 ,可得AP=2,
,可得AP=2, .
.又∵PN=4,∴可得AN=6,
∴点N的坐标为
 .
.把
 代入
代入 中,得k=9.
中,得k=9.(2)∵k=9,∴双曲线方程为
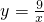 .
.当x=2时,
 .∴
.∴ .
.又∵PM⊥AN,
∴AM=
 =
=
∴C△APM=5+
 .
.分析:(1)寻找经过双曲线
 的点的坐标,由P点的坐标入手,可求的N点的坐标,代入即可得出K的值.
的点的坐标,由P点的坐标入手,可求的N点的坐标,代入即可得出K的值.(2)求△APM的周长,先求出各个边的长度,AP的长度为P点的横坐标已知,MP的长度为M的纵坐标减去P的纵坐标,再利用勾股定理求出AM即可.
点评:本题通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )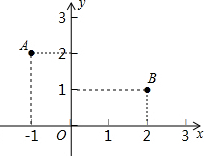 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )