题目内容
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 、
、![]() 上分别找点
上分别找点![]() 、
、![]() ,使
,使![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转,
顺时针方向旋转,![]() 的中点
的中点![]() 恰好落在
恰好落在![]() 的中点,延长
的中点,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
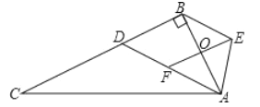
(1)四边形![]() 是什么特殊四边形?说明理由.
是什么特殊四边形?说明理由.
(2)是否存在![]() 中,使得图中四边形
中,使得图中四边形![]() 为菱形?若不存在,说明理由;若存在,求出此时
为菱形?若不存在,说明理由;若存在,求出此时![]() 的面积与
的面积与![]() 面积的倍数关系.
面积的倍数关系.
【答案】(1)四边形![]() 是平行四边形,理由见解析;(2)存在,
是平行四边形,理由见解析;(2)存在,![]() ,理由见解析.
,理由见解析.
【解析】
(1)由于AE=AF,且O是EF中点,根据等腰三角形三线合一的性质知:AO⊥EF,即FO∥BD,从而证得OF是△ABD的中位线,由此可得BD=2OF=EF,那么BD、EF平行且相等,根据一组对边平行且相等的四边形是平行四边形即可判断出四边形BDFE的形状.
(2)当四边形BDFE是菱形时,BD=FD,即AF=2BD,由此可得∠FAO=30°,∠BAC=∠EAF=60°;易证得△FOA∽△ABC,首先求出FO、OA即FO、AB的比例关系,即可得到△AFO、△ABC的面积比,进而可得到△AEF、△ABC的面积比.
解:(1)四边形![]() 是平行四边形;
是平行四边形;
理由:∵![]() ,且
,且![]() 是
是![]() 中点,
中点,
∴![]() ,即
,即![]() ;
;
∵![]() 是
是![]() 中点,
中点,
∴![]() 是
是![]() 的中位线,即
的中位线,即![]() ,
,
∴![]() 、
、![]() 平行且相等,
平行且相等,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)若四边形![]() 是菱形,则
是菱形,则![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,即
,即![]() ;
;
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
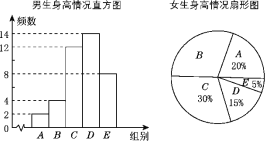
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在________组(填组别序号),女生身高在B组的人数有________人;
(2)在样本中,身高在150≤x<155之间的人数共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人、女生480人,请估计身高在155≤x<165之间的学生有多少人