题目内容
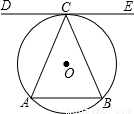
如图，AB是圆O的弦，直线DE切圆O于点C，AC=BC，
求证：DE∥AB．
证明：∵AC=BC，
∴∠A=∠B．
又∵DE是圆O的切线，
∴∠ACD=∠B（弦切角等于它所夹的弧所对得圆周角），
∴∠A=∠ACD，
∴AB∥DE．
分析：先根所等边对等角得到∠A=∠B，再根据同一弧所对的圆周角相等得到∠ACD=∠B，从而得出∠A=∠ACD，那么AB∥DE．
点评：此题主要考查学生对切线的性质及等腰三角形的性质的掌握情况．
∴∠A=∠B．
又∵DE是圆O的切线，
∴∠ACD=∠B（弦切角等于它所夹的弧所对得圆周角），
∴∠A=∠ACD，
∴AB∥DE．
分析：先根所等边对等角得到∠A=∠B，再根据同一弧所对的圆周角相等得到∠ACD=∠B，从而得出∠A=∠ACD，那么AB∥DE．
点评：此题主要考查学生对切线的性质及等腰三角形的性质的掌握情况．
练习册系列答案
相关题目
21、如图，AB是圆O的弦，直线DE切圆O于点C，AC=BC，
