题目内容
一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
(1);(2)P(两次摸到红球)=. 【解析】试题分析:(1)根据4个小球中红球的个数,即可确定出从中任意摸出1个球,恰好摸到红球的概率; (2)列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率. 试题解析:(1)4个小球中有2个红球, 则任意摸出1个球,恰好摸到红球的概率是; (2)列表如下: 红 红 ...
练习册系列答案
相关题目
二次函数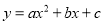 图象上部分点的坐标满足下表,则该函数图象的顶点坐标为
图象上部分点的坐标满足下表,则该函数图象的顶点坐标为
X | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
A. (﹣3,﹣3) B. (﹣2,﹣2) C. (﹣1,﹣3) D. (0,﹣6)
B 【解析】∵x=?3和?1时的函数值都是?3相等, ∴二次函数的对称轴为直线x=?2, ∴顶点坐标为(?2,?2). 故选:B.

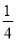
 的图像向右平移1个单位长度,再向上平移3个单位长度,所得图像的函数关系式是____________________.
的图像向右平移1个单位长度,再向上平移3个单位长度,所得图像的函数关系式是____________________.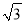 ﹣2)0﹣(﹣1)2017+
﹣2)0﹣(﹣1)2017+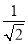 ﹣sin45°;
﹣sin45°; 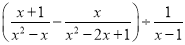 .
.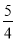 b)元 B. (a+
b)元 B. (a+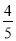 b)元 C. (b+
b)元 C. (b+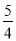 a)元 D. (b+
a)元 D. (b+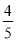 a)元
a)元