题目内容
在直角梯形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 .
【答案】分析:首先由已知AD∥BC,∠ABC=90°点E是BC边的中点,推出四边形ABED是矩形,所以得到直角三角形CED,所以能求出CD和DE,又由△DEF是等边三角形,得出DF,由Rt△AGD可求出AG、DG,进而求得FG,再证△AGD≌△FGB,得到BF=AD,从而求出△BFG的周长.
解答:解:∵AD∥BC,∠ABC=90°,点E是BC边的中点,
∴AD=BE=CE=1,
∴四边形ABED为平行四边形,
∴∠DEC=90°,∠A=90°,
又∵∠C=60°,
∴DE=CE•tan60°=1× =
= ,
,
又∵△DEF是等边三角形,
∴DF=DE=AB= ,∠AGD=∠EDF=60°,∠ADG=30°,
,∠AGD=∠EDF=60°,∠ADG=30°,
∴AG=AD•tan30°=1× =
= ,
,
∴DG=2AG= ,FG=DF-DG=
,FG=DF-DG= -
- =
= ,
,
BG=AB-AG= -
- =
= ,
,
∵在△AGD与△FGB中,
 ,
,
∴△AGD≌△FGB,
∴BF=AD=1,
∴△BFG的周长为=FG+BG+BF= +
+ +1=1+
+1=1+ .
.
故答案为:1+ .
.
点评:本题考查的是直角梯形,涉及到等边三角形的性质及解直角三角形,熟知等边三角形的性质是解答此题的关键.
解答:解:∵AD∥BC,∠ABC=90°,点E是BC边的中点,
∴AD=BE=CE=1,
∴四边形ABED为平行四边形,
∴∠DEC=90°,∠A=90°,
又∵∠C=60°,
∴DE=CE•tan60°=1×
 =
= ,
,又∵△DEF是等边三角形,
∴DF=DE=AB=
 ,∠AGD=∠EDF=60°,∠ADG=30°,
,∠AGD=∠EDF=60°,∠ADG=30°,∴AG=AD•tan30°=1×
 =
= ,
,∴DG=2AG=
 ,FG=DF-DG=
,FG=DF-DG= -
- =
= ,
,BG=AB-AG=
 -
- =
= ,
,∵在△AGD与△FGB中,

 ,
,∴△AGD≌△FGB,
∴BF=AD=1,
∴△BFG的周长为=FG+BG+BF=
 +
+ +1=1+
+1=1+ .
.故答案为:1+
 .
.点评:本题考查的是直角梯形,涉及到等边三角形的性质及解直角三角形,熟知等边三角形的性质是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
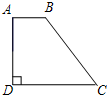 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
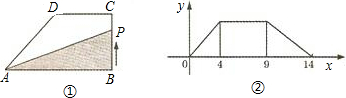
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )