题目内容
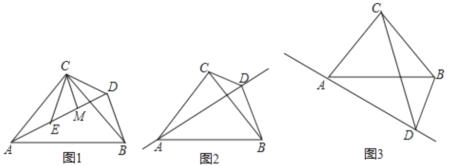
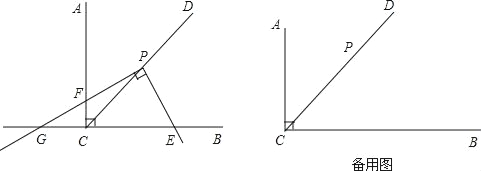
【题目】已知,∠ACB=90°,CD是∠ACB的平分线,点P在CD上,CP=![]() .将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
(1)如图,当点F在射线CA上时,
①求证:PF=PE.
②设CF=x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)连接EF,当△CEF与△EGP相似时,求EG的长.
【答案】(1)①见解析,②![]() (0≤x<1);(2)当△CEF与△EGP相似时,①当点F在射线CA上时,EG=2
(0≤x<1);(2)当△CEF与△EGP相似时,①当点F在射线CA上时,EG=2![]() ,②当点F在AC延长线上时,EG=2
,②当点F在AC延长线上时,EG=2![]() .
.
【解析】
(1)①过点P作PM⊥AC,PN⊥BC,垂足分别为M、N,由已知条件证明△PMF≌△PNE即可证明PF=PE;②利用①中的三角形全等和相似三角形的性质即可求出y与x的函数解析式,再写出其自变量的取值范围即可;
(2)当△CEF与△EGP相似时,点F的位置有两种情况:①当点F在射线CA上时,②当点F在AC延长线上时,分别讨论求出满足题意的EG长即可.
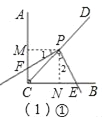
(1)①过点P作PM⊥AC,PN⊥BC,垂足分别为M、N,
∵CD是∠ACB的平分线,
∴PM=PN,
由∠PMC=∠MCN=∠CNP=90°,得∠MPN=90°,
∴∠1+∠FPN=90°,
∵∠2+∠FPN=90°,
∴∠1=∠2,
∴△PMF≌△PNE,
∴PF=PE;
②∵CP=![]() ,
,
∴CN=CM=1.
∵△PMF≌△PNE,
∴NE=MF=1﹣x.
∴CE=2﹣x.
∵CF∥PN,
∴△GCF∽△GNP,
∴![]() .
.
∴![]() .
.
∴![]() (0≤x<1).
(0≤x<1).
(2)当△CEF与△EGP相似时,点F的位置有两种情况:
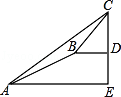
①当点F在射线CA上时,
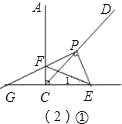
∵∠GPE=∠FCE=90°,∠1≠∠PEG,
∴∠G=∠1.
∴FG=FE.
∴CG=CE.
在Rt△EGP中,EG=2CP=2![]() ;
;
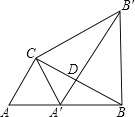
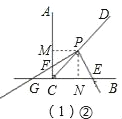
②当点F在AC延长线上时,
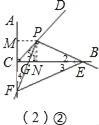
∵∠GPE=∠FCE=90°,∠1≠∠2,
∴∠3=∠2,
∵∠1=45°+∠5,∠1=45°+∠2,
∴∠5=∠2,
易证∠3=∠4,可得∠5=∠4,
∴FC=CP=![]() ,
,
∴FM=1+![]() ,
,
易证△PMF≌△PNE,
可得EN=1+![]() ,
,
∵CF∥PN,
![]() ,
,
∴GN=![]() ﹣1.
﹣1.
∴EG=2![]() .
.

【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造![]() 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
型号 | 占地面积( | 使用农户数(户/个) | 造价(万元/个) |
|
|
|
|
|
|
|
|
已知可供建造沼气池的占地面积不超过![]() ,该村农户共有492户.
,该村农户共有492户.
(1)满足条件的方案共有几种?写出解答过程;
(2)通过计算判断,哪种建造方案最省钱.
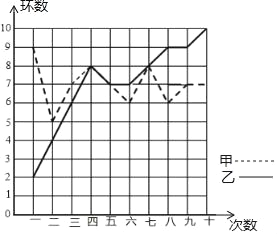
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.