题目内容
【题目】在平面直角坐标系![]() 中(如图),点
中(如图),点![]() 为直线
为直线![]() 和双曲线
和双曲线![]() 的一个交点,
的一个交点,
(1)求![]() 、
、![]() 的值;
的值;
(2)若点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,使得
,使得![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在双曲线是否存在点![]() ,使得
,使得![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在请说明理由。
的坐标;若不存在请说明理由。

【答案】(1)k=-![]() ,m=-4;(2)点P的坐标为(4,-1)或(-12,3);(3)M(
,m=-4;(2)点P的坐标为(4,-1)或(-12,3);(3)M(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法即可解决问题.
(2)如图1中,设直线y=-![]() x与反比例函数y=-
x与反比例函数y=-![]() 的另一个交点为C(4,-1).由对称性可知:OA=OC,推出当点P与C重合时,S△ABP=2S△ABO,此时P(4,-1).当点P在OA的延长线上时,P′A=AC时,S△ABP=2S△ABO,再利用中点坐标公式求解即可.
的另一个交点为C(4,-1).由对称性可知:OA=OC,推出当点P与C重合时,S△ABP=2S△ABO,此时P(4,-1).当点P在OA的延长线上时,P′A=AC时,S△ABP=2S△ABO,再利用中点坐标公式求解即可.
(3)如图2中,将OA绕点O顺时针旋转90°得到OA′,则A′(1.4),取AA′的中点D,作直线OD在第二象限交反比例函数于M.此时∠AOM=45°,求出直线OD的解析式,再构建方程组确定点M的坐标.
(1)∵点A(-4,1)在直线y=kx和双曲线y=![]() 的图象上,
的图象上,
∴k=-![]() ,m=-4.
,m=-4.
(2)如图1中,设直线y=-![]() x与反比例函数y=-
x与反比例函数y=-![]() 的另一个交点为C(4,-1).
的另一个交点为C(4,-1).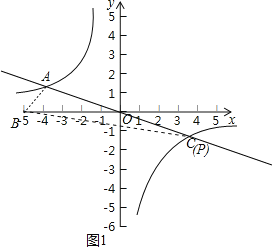
由对称性可知:OA=OC,
∴当点P与C重合时,S△ABP=2S△ABO,此时P(4,-1).
当点P在OA的延长线上时,P′A=AC时,S△ABP=2S△ABO,此时P′(-12,3),
综上所述,满足条件的点P的坐标为(4,-1)或(-12,3).
(3)如图2中,将OA绕点O顺时针旋转90°得到OA′,则A′(1.4),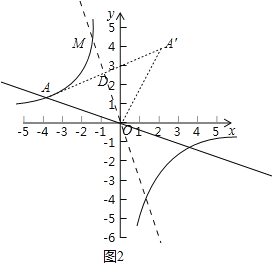
取AA′的中点D,作直线OD在第二象限交反比例函数于M.此时∠AOM=45°,
∵D(-![]() ),
),
∴直线OD的解析式为y=-![]() x,
x,
由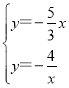 ,解得
,解得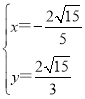 或
或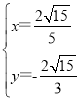 ,
,
∵点M在第二象限,
∴M(![]() ,
,![]() ).
).

练习册系列答案
相关题目