题目内容
(2004•扬州)下列英文大写字母中既是轴对称图形又是中心对称图形的是( )A.E
B.M
C.N
D.H
【答案】分析:根据轴对称图形和中心对称图形的概念求解.
解答:解:字母E和M都只是轴对称图形,字母N是中心对称图形,字母H既是轴对称图形又是中心对称的图形.
故选D.
点评:此题是跨学科题目,结合英语知识考查了轴对称图形和中心对称图形的概念.
【链接】轴对称图形:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形;
中心对称图形:在同一平面内,如果把一个图形绕某一点旋转180°,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.
解答:解:字母E和M都只是轴对称图形,字母N是中心对称图形,字母H既是轴对称图形又是中心对称的图形.
故选D.
点评:此题是跨学科题目,结合英语知识考查了轴对称图形和中心对称图形的概念.
【链接】轴对称图形:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形;
中心对称图形:在同一平面内,如果把一个图形绕某一点旋转180°,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.

练习册系列答案
相关题目
(2004•扬州)据电力部门统计,每天8:00至21:00是用电高峰期,简称“峰时”,21:00至次日8:00是用电低谷期,简称“谷时”.为了缓解供电需求紧张的矛盾,我市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策.具体见下表:
已知每千瓦时峰时价比谷时价高0.25元.小卫家对换表后最初使用的100千瓦时用电情况进行统计分析知:峰时用电量占80%,谷时用电量占20%,与换表前相比,电费共下降2元.
(1)请你求出表格中x和y的值;?
(2)小卫希望通过调整用电时间,使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元(包括10元和15元).假设小卫家今后“峰时”用电量占整个家庭用电量的z%,那么,z在什么范围内时,才能达到小卫的期望?
| 时间 | 换表前 | 换表后 | |
| 峰时(8:00-21:00) | 谷时(21:00-次日8:00) | ||
| 电价 | 0.52元/千瓦时 | x元/千瓦时 | y元/千瓦时 |
(1)请你求出表格中x和y的值;?
(2)小卫希望通过调整用电时间,使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元(包括10元和15元).假设小卫家今后“峰时”用电量占整个家庭用电量的z%,那么,z在什么范围内时,才能达到小卫的期望?
(2004•扬州)据电力部门统计,每天8:00至21:00是用电高峰期,简称“峰时”,21:00至次日8:00是用电低谷期,简称“谷时”.为了缓解供电需求紧张的矛盾,我市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策.具体见下表:
已知每千瓦时峰时价比谷时价高0.25元.小卫家对换表后最初使用的100千瓦时用电情况进行统计分析知:峰时用电量占80%,谷时用电量占20%,与换表前相比,电费共下降2元.
(1)请你求出表格中x和y的值;?
(2)小卫希望通过调整用电时间,使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元(包括10元和15元).假设小卫家今后“峰时”用电量占整个家庭用电量的z%,那么,z在什么范围内时,才能达到小卫的期望?
| 时间 | 换表前 | 换表后 | |
| 峰时(8:00-21:00) | 谷时(21:00-次日8:00) | ||
| 电价 | 0.52元/千瓦时 | x元/千瓦时 | y元/千瓦时 |
(1)请你求出表格中x和y的值;?
(2)小卫希望通过调整用电时间,使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元(包括10元和15元).假设小卫家今后“峰时”用电量占整个家庭用电量的z%,那么,z在什么范围内时,才能达到小卫的期望?
 ),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.
),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.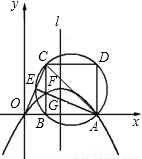
 ),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.
),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.