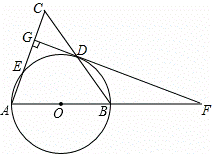
题目内容
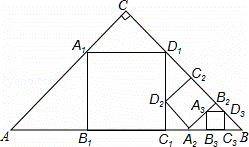
如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为 .
( )na
)na
解答: 解:设正方形A1B1C1D1的边长为x,
∵△CA1D1和△AA1B1都是等腰直角三角形,
∴A1C= x,AA1=
x,AA1= x,
x,
∴ x+
x+ x=a,解得x=
x=a,解得x= a,
a,
即第1个正方形的边长为 a,
a,
设正方形A2B2C2D2的边长为y,
∵△C2D1D2和△C1A2D2都是等腰直角三角形,
∴C1D2= y,D1D2=
y,D1D2= y,
y,
∴ y+
y+ y=
y= a,解得y=(
a,解得y=( )2a,
)2a,
即第2个正方形的边长为( )2a,
)2a,
同理可得第3个正方形的边长为( )3a,
)3a,
∴第n个正方形的边长为( )na.
)na.
故答案为( )na.
)na.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出
 的解集是 .
的解集是 . =
= ×2 B.
×2 B.  ﹣35
﹣35 ﹣
﹣ =35
=35 ,求CG的长.
,求CG的长.