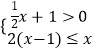Question

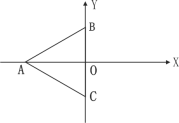
【题目】如图，等边三角形ABC的顶点B（0，2），A在x轴负半轴上、C在y轴负半轴上.

（1）写出A、C两点的坐标；

（2）求△ABC的面积和周长.

Answer 1

【答案】（1）A（-，0），C（0，-2）；（2）S△ABC =,周长为12.

【解析】

(1)由等边三角形的性质可知原点是BC的中点,OA是三角形的高, 通过解直角三角形即可求得A、C的坐标;

(2) 根据B、C的坐标求得正三角形的边长, 然后根据面积公式和周长公式即可求得;

解：(1)等边△ABC的顶点B的坐标(0,2),A在x轴负半轴上、C在y轴负半轴上B、C在y轴上.

x轴垂直平分BC,A0是BC边上的高,

OA平分∠BAC,

∠BAO=30,

OA=tan30 OA=2= ,

A(-,0),C(0,-2) ;

(2)B(-,0),C(0,-2) ;,

BC=4,

=== ,周长=3BC=34=12 ;