题目内容
【题目】如图，在边长为1的小正方形组成的网格中，四边形ABCD的四个顶点都在格点上，请按要求完成下列各题．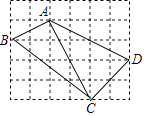 
（1）线段AB的长为 ， BC的长为 ， CD的长为；
（2）连接AC，通过计算说明△ACD和△ABC是什么特殊三角形．
【答案】
（1）
；5；2 
（2）解：∵AC= 
=2 ，AD= =2 ，
∴AC=AD，
∴△ACD是等腰三角形；
∵AB2+AC2=5+20=25=BC2，
∴△ABC是直角三角形
【解析】解：（1）由勾股定理得：AB= 
= ，BC= 
=5，CD= 
=2 ； 所以答案是： ，5，2 ；
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对勾股定理的逆定理的理解，了解如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
相关题目
