题目内容
已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图.
(1)若BD是AC的中线,求
| BD |
| CE |
(2)若BD是∠ABC的角平分线,求
| BD |
| CE |
(3)结合(1)、(2),试推断
| BD |
| CE |
| BD |
| CE |
| 4 |
| 3 |
分析:先设AB=AC=2a,CD=a,则BC=
a,AD=a.求出BD,又求得Rt△ABD∽Rt△ECD,
(1)BD是AC的中线,则CD=AD=x=
,则解得;
(2)BD是∠ABC的角平分线,则求得x,y值;
(3)由以上两个问题,从
的比值求得x的值,则求得
的值.
| 2 |
(1)BD是AC的中线,则CD=AD=x=
| 1 |
| 2 |
(2)BD是∠ABC的角平分线,则求得x,y值;
(3)由以上两个问题,从
| DB |
| CE |
| AD |
| CD |
解答:解:设CD=AD=a,则AB=AC=2a.
(1)在Rt△ABD中,由勾股定理得:BD=
a,
∵∠A=∠E=90°,∠ADB=∠EDC,
∴△BAD∽△CED,
∴
=
,
∴
=
,
解得:CE=
,
∴
=
=
;
(2)过点D作DF⊥BC于F,
∵BD是∠ABC的平分线,
∴AD=DF,
∵在Rt△ABC中,cos∠ABC=
=
,
在Rt△CDF中,sin∠DCF=
=
,
即
=
=
,
∴
=
,
即
=
,
∴CD=2(2-
)a,
∴AD=AC-CD=2a-2(2-
)a=2(
-1)a,
∴BD2=AD2+AB2=8(2-
)a2,
∵Rt△ABD∽Rt△CED,
∴CE=
=
a2.
∴
=
=
=2.
(3)当D在A点时,
=1,
当D越来越接近C时,
越来越接近无穷大,
∴
的取值范围是
≥1.
设AB=AC=1,CD=x,AD=1-x,
在Rt△ABD中,BD2=12+(1-x)2,
又∵Rt△ABD∽Rt△ECD,
∴
=
,即
=
,
解得:CE=
,
若y=
=x+
-2=
,则有3x2-10x+6=0,
∵0<x≤1,
∴解得x=
∴
=
=
,
表明随着点D从A向C移动时,BD逐渐增大,而CE逐渐减小,
的值则随着D从A向C移动而逐渐增大,
∴探究
的值能小于
,此时AD=
CD.
(1)在Rt△ABD中,由勾股定理得:BD=
| 5 |
∵∠A=∠E=90°,∠ADB=∠EDC,
∴△BAD∽△CED,
∴
| BD |
| CD |
| AB |
| CE |
∴
| ||
| a |
| 2a |
| CE |
解得:CE=
| 2a | ||
|
∴
| BD |
| CE |
| ||||
|
| 5 |
| 2 |
(2)过点D作DF⊥BC于F,
∵BD是∠ABC的平分线,
∴AD=DF,
∵在Rt△ABC中,cos∠ABC=
| AB |
| BC |
| ||
| 2 |
在Rt△CDF中,sin∠DCF=
| DF |
| CD |
| ||
| 2 |
即
| AD |
| CD |
| AB |
| BC |
| ||
| 2 |
∴
| AD+CD |
| CD |
2+
| ||
| 2 |
即
| 2a |
| CD |
2+
| ||
| 2 |
∴CD=2(2-
| 2 |
∴AD=AC-CD=2a-2(2-
| 2 |
| 2 |
∴BD2=AD2+AB2=8(2-
| 2 |
∵Rt△ABD∽Rt△CED,
∴CE=
| AB•CD |
| BD |
4(2-
| ||
| BD |
∴
| BD |
| CE |
| BD | ||||
|
| BD2 | ||
4(2-
|

(3)当D在A点时,
| BD |
| CE |
当D越来越接近C时,
| BD |
| CE |
∴
| BD |
| CE |
| BD |
| CE |
设AB=AC=1,CD=x,AD=1-x,
在Rt△ABD中,BD2=12+(1-x)2,
又∵Rt△ABD∽Rt△ECD,
∴
| CE |
| AB |
| CD |
| BD |
| CE |
| 1 |
| x | ||
|
解得:CE=
| x | ||
|
若y=
| BD |
| CE |
| 2 |
| x |
| 4 |
| 3 |
∵0<x≤1,
∴解得x=
5-
| ||
| 3 |
∴
| AD |
| DC |
| 1-x |
| x |
| ||
| 6 |
表明随着点D从A向C移动时,BD逐渐增大,而CE逐渐减小,
| BD |
| CE |
∴探究
| BD |
| CE |
| 4 |
| 3 |
| ||
| 6 |
点评:本题考查了相似三角形的判定和性质,本题从中线,角平分线以及中线与角平线相结合的问题来考查,是一道考查全面的好题.

练习册系列答案
相关题目
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.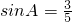 ,其中A为锐角,试求sadA的值;
,其中A为锐角,试求sadA的值;