题目内容
 一枚商标的图案如图所示,点A1,A2,A3,A4和C1,C2,C3,C4分别是?ABCD边AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知?ABCD的面积5,则影阴四边形A4B2C4D2的面积是
一枚商标的图案如图所示,点A1,A2,A3,A4和C1,C2,C3,C4分别是?ABCD边AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知?ABCD的面积5,则影阴四边形A4B2C4D2的面积是3
3
.分析:可以设平行四边形ABCD的面积是S,根据等分点的定义利用平行四边形ABCD的面积减去四个角上的三角形的面积,就可表示出四边形A4B2C4D2的面积,从而得到两个四边形面积的关系,即可求解.
解答:解:设平行四边形ABCD的面积是S,设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y.
则S=5a•3x=3b•5y.即ax=by=
.
△AA4D2与△B2CC4全等,B2C=
BC=b,B2C边上的高是
•5y=4y.
则△AA4D2和△B2CC4的面积是2by=
.
同理△D2C4D与△A4BB2的面积是
.
则四边形A4B2C4D2的面积是S-
-
=
,
又∵S=9,
∴四边形A4B2C4D2的面积=
×5=3.
故答案为:3.
则S=5a•3x=3b•5y.即ax=by=
| S |
| 15 |
△AA4D2与△B2CC4全等,B2C=
| 1 |
| 3 |
| 4 |
| 5 |
则△AA4D2和△B2CC4的面积是2by=
| 2S |
| 15 |
同理△D2C4D与△A4BB2的面积是
| S |
| 15 |
则四边形A4B2C4D2的面积是S-
| 2S |
| 15 |
| S |
| 15 |
| 9S |
| 15 |
又∵S=9,
∴四边形A4B2C4D2的面积=
| 9 |
| 15 |
故答案为:3.
点评:此题考查平行四边形的性质和三角形面积计算,正确利用等分点的定义,得到两个四边形的面积的关系是解决本题的关键,难度较大.

练习册系列答案
相关题目
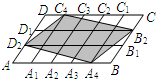 一枚商标的图案如图所示,点A1,A2,A3,A4和C1,C2,C3,C4分别是?ABCD边AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知?ABCD的面积5,则影阴四边形A4B2C4D2的面积是________.
一枚商标的图案如图所示,点A1,A2,A3,A4和C1,C2,C3,C4分别是?ABCD边AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知?ABCD的面积5,则影阴四边形A4B2C4D2的面积是________.