题目内容
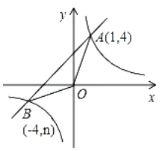
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)写出点![]() 所在直线的函数解析式;
所在直线的函数解析式;
(2)连接![]() ,若线段
,若线段![]() 能构成三角形,求
能构成三角形,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 把四边形
把四边形![]() 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 时,线段
时,线段![]() 能构成三角形;(3)当
能构成三角形;(3)当![]() 时,
时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分.
的面积分成相等的两部分.
【解析】
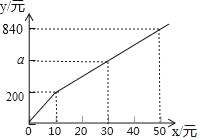
(1)根据题意可得点![]() ,可得的当横坐标为m时,纵坐标为-3m+22,因此可得点C的所在直线的解析式.
,可得的当横坐标为m时,纵坐标为-3m+22,因此可得点C的所在直线的解析式.
(2)首先利用待定系数法计算直线AB的解析式,再利用点C是否在直线上,来确定是否构成三角形,从而确定m的范围.
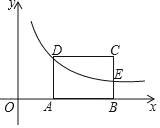
(3)首先计算D点坐标,设![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]()
![]() 轴于
轴于![]() ,
,![]()
![]() 轴于
轴于![]() ,进而确定E点的坐标,再计算DE所在直线的解析式,根据点C在直线DE上可求得m的值.
,进而确定E点的坐标,再计算DE所在直线的解析式,根据点C在直线DE上可求得m的值.
解:(1)根据题意可得点![]() ,可得的当横坐标为m时,纵坐标为-3m+22,所以
,可得的当横坐标为m时,纵坐标为-3m+22,所以![]()
(2)设![]() 所在直线的函数解析式为
所在直线的函数解析式为![]() ,将点
,将点![]() ,
,![]() 代入
代入![]() 得
得
![]() ,解得
,解得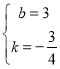 ,∴
,∴![]()
当点![]() 在直线
在直线![]() 上时,线段
上时,线段![]() 不能构成三角形
不能构成三角形
将![]() 代入
代入![]() ,得
,得![]()
解得![]() ,
,
∴![]() 时,线段
时,线段![]() 能构成三角形;
能构成三角形;
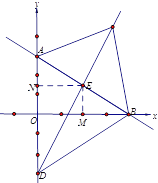
(3)根据题意可得![]() ,
,
设![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]()
![]() 轴于
轴于![]() ,
,![]()
![]() 轴于
轴于![]() ,
,
根据三角形中位线性质可知![]() ,由三角形中线性质可知,当点
,由三角形中线性质可知,当点![]() 在直线
在直线![]() 上时,
上时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分,
的面积分成相等的两部分,
设直线![]() 的函数解析式为
的函数解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,
,
得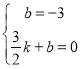 ,解得
,解得![]() ,∴
,∴![]() ,
,
将![]() 代入
代入![]() ,得
,得
![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分.
的面积分成相等的两部分.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位:m):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
跑步情况(m) | +420 | +460 | -100 | -210 | -330 | +200 | -240 |
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分,求本周内小明用于跑步的时间.