Question

如图，已知AB=AC，∠BAC=120º，在BC上取一点O，以O为圆心OB为半径作圆，
①且⊙O过A点，过A作AD∥BC交⊙O于D，
求证：（1）AC是⊙O的切线；
（2）四边形BOAD是菱形。

Answer 1

证明：（1）∵AB=AC，∠BAC=120º，∴∠ABC=∠C=30º。
∵OB=OA，∴∠BAO=∠ABC=30º。∴∠CAO=120º-30º=90º。
∴ OA⊥AC。
∵OA为⊙O的半径，∴ AC是⊙O的切线。
（2）连接OD，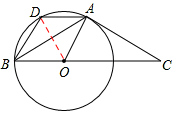

∵AD∥BC，
∴∠DAB=∠ABC=30º。
∴∠DAO=60º。
∵OA=OD，∴△OAD为等边三角形。
∴OB=OA=AD，
又∵AD∥BC，∴ADBO为平行四边形。
且OA=OB，∴四边形BOAD是菱形。

解析