题目内容
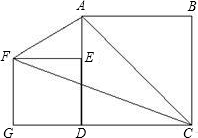
在边长为4的正方形ABCD中，以点B为圆心，BA为半径作弧
，F为
上的一动点，过点F作⊙B的切线交AD于点P，交DC于点Q．
（1）求证△DPQ的周长等于正方形ABCD的周长的一半；
（2）分别延长PQ、BC，延长线相交于点M，设AP长为x，BM长为y，试求出y与x之间的函数关系式．
 |
| AC |
|
| AC |
（1）求证△DPQ的周长等于正方形ABCD的周长的一半；
（2）分别延长PQ、BC，延长线相交于点M，设AP长为x，BM长为y，试求出y与x之间的函数关系式．
（1）证明：∵正方形ABCD，
∴∠DAB=∠D=∠DCB=90°，
即AB=BC=CD=AD，AB⊥AD，BC⊥CD，
∴DA和CD都是圆B的切线，
∵PQ切圆B于F，
∴AP=PF，QF=CQ，
∴△DPQ的周长是DP+DQ+PQ=DP+DQ+PF+QF=DP+AP+DQ+CQ=AD+CD，
∵正方形ABCD的周长是AD+AB+CD+BC=2AD+2CD，
∴△DPQ的周长等于正方形ABCD的周长的一半．
（2）在Rt△PDQ中，由勾股定理得：DP2+DQ2=PQ2，
∴（4-x）2+（4-CQ）2=（X+CQ）2，
解得：CQ=
，
DQ=4-
=
，
∵正方形ABCD，
∴AD∥BC，
∴△PDQ∽△MCQ，
∴
=
，
即
=
，
∴y=
+
x，
y与x之间的函数关系式是y=
+
x．
∴∠DAB=∠D=∠DCB=90°，
即AB=BC=CD=AD，AB⊥AD，BC⊥CD，
∴DA和CD都是圆B的切线，
∵PQ切圆B于F，
∴AP=PF，QF=CQ，
∴△DPQ的周长是DP+DQ+PQ=DP+DQ+PF+QF=DP+AP+DQ+CQ=AD+CD，
∵正方形ABCD的周长是AD+AB+CD+BC=2AD+2CD，
∴△DPQ的周长等于正方形ABCD的周长的一半．
（2）在Rt△PDQ中，由勾股定理得：DP2+DQ2=PQ2，
∴（4-x）2+（4-CQ）2=（X+CQ）2，
解得：CQ=
| 16-4x |
| x+4 |
DQ=4-
| 16-4x |
| x+4 |
| 8x |
| x+4 |
∵正方形ABCD，
∴AD∥BC，
∴△PDQ∽△MCQ，
∴
| DP |
| CM |
| DQ |
| CQ |
即
| 4-x |
| y-4 |
| ||
|
∴y=
| 8 |
| x |
| 1 |
| 2 |
y与x之间的函数关系式是y=
| 8 |
| x |
| 1 |
| 2 |
练习册系列答案
怎样学好牛津英语系列答案
相关题目
正方形？请简要说明你的理由．
