题目内容
已知方程ax2+2x+c=0(a≠0)有两个正实数根,则P(a,c)关于x轴的对称点P′在第
二
二
象限.分析:利用根与系数的关系得出a,c的符号,进而得出P点所在象限,即可得出关于x轴对称点位置.
解答:解:∵方程ax2+2x+c=0(a≠0)有两个正实数根,
∴x1+x2=-
>0,x1×x2=
>0,
∴a<0,c<0,
∴P点在第三象限,
∴P(a,c)关于x轴的对称点P′在第二象限.
故答案为;二.
∴x1+x2=-
| 2 |
| a |
| c |
| a |
∴a<0,c<0,
∴P点在第三象限,
∴P(a,c)关于x轴的对称点P′在第二象限.
故答案为;二.
点评:此题主要考查了根与系数的关系以及关于x轴对称点的性质,得出a,c的符号是解题关键.

练习册系列答案
相关题目
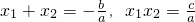 .我们把一元二次方程的根与系数关系的这个结论称为“韦达定理”.根据这个结论解决下面问题:
.我们把一元二次方程的根与系数关系的这个结论称为“韦达定理”.根据这个结论解决下面问题: ;
;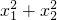 ;
; ;
;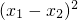 .
.