题目内容
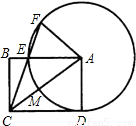
(2002•吉林)如图,已知矩形ABCD,以A为圆心,AD为半径的圆交AC、AB于M、E,CE的延长线交⊙A于F,CM=2,AB=4.(1)求⊙A的半径;(2)求CE的长和△AFC的面积.
【答案】分析:(1)先根据切割线定理求出CA的长,然后在Rt△ACD中,用勾股定理求出AB即⊙O的半径长;
(2)在Rt△BCE中,根据勾股定理,易求得CE的长;由切割线定理得CD2=CE•CF,由此可求出CF和EF的长;在△AFC中,已知底边CF的长,关键是求出CF边上的高;过A作AG⊥CF于G,通过相似三角形△AEG和△CEB得出的成比例线段可求出AG的长;由此可根据三角形的面积公式求得△AFC的面积.
解答: 解:(1)四边形ABCD为矩形,AB=4;∴CD=4.
解:(1)四边形ABCD为矩形,AB=4;∴CD=4.
在Rt△ACD中,AC2=CD2+AD2;
∴(2+AD)2=42+AD2;
解得AD=3.
(2)过A点作AG⊥EF于G;
∵BC=3,BE=AB-AE=4-3=1.
∴CE= =
= =
= .
.
由CE•CF=CD2,得:
CF= =
= =
=
 .
.
又∵∠B=∠AGE=90°,∠BEC=∠GEA,
∴△BCE∽△GAE;
∴ ,即
,即 =
= .
.
∴AG=
 .
.
∴S△AFC= CF•AG=
CF•AG= ×
×
 ×
×
 =
= .
.
点评:本题主要考查的是切割线定理、矩形的性质、勾股定理、相似三角形的判定和性质等知识.
(2)在Rt△BCE中,根据勾股定理,易求得CE的长;由切割线定理得CD2=CE•CF,由此可求出CF和EF的长;在△AFC中,已知底边CF的长,关键是求出CF边上的高;过A作AG⊥CF于G,通过相似三角形△AEG和△CEB得出的成比例线段可求出AG的长;由此可根据三角形的面积公式求得△AFC的面积.
解答:
 解:(1)四边形ABCD为矩形,AB=4;∴CD=4.
解:(1)四边形ABCD为矩形,AB=4;∴CD=4.在Rt△ACD中,AC2=CD2+AD2;
∴(2+AD)2=42+AD2;
解得AD=3.
(2)过A点作AG⊥EF于G;
∵BC=3,BE=AB-AE=4-3=1.
∴CE=
 =
= =
= .
.由CE•CF=CD2,得:
CF=
 =
= =
=
 .
.又∵∠B=∠AGE=90°,∠BEC=∠GEA,
∴△BCE∽△GAE;
∴
 ,即
,即 =
= .
.∴AG=

 .
.∴S△AFC=
 CF•AG=
CF•AG= ×
×
 ×
×
 =
= .
.点评:本题主要考查的是切割线定理、矩形的性质、勾股定理、相似三角形的判定和性质等知识.

练习册系列答案
相关题目
 、
、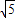 (在图(1))中画一个即可);
(在图(1))中画一个即可);