Question

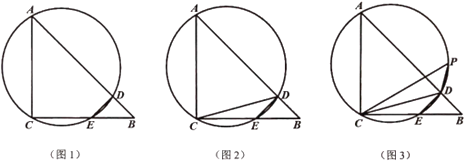
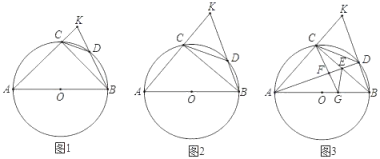
【题目】已知AB是⊙O的直径，点C是弧AB的中点，点D在弧BC上，BD、AC的延长线交于点K，连接CD．

（1）求证：∠AKB﹣∠BCD＝45°；

（2）如图2，若DC＝DB时，求证：BC＝2CK；

（3）在（2）的条件下，连接BC交AD于点E，过点C作CF⊥AD于点F，延长CF交AB于点G，连接GE，若GE＝5，求CD的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）CD＝6．

【解析】

（1）连接AD，先证△ABC是等腰直角三角形得∠CAB＝∠CBA＝45°，设∠CBK＝∠DAC＝α，则∠DAB＝∠DCB＝45°α，∠K＝90°α，据此可得；

（2）过点C作CH⊥AD，先证△EBD≌△EHC可得CE＝BE＝BC，再证△ACE≌△BCK得CK＝CE，从而得证；

（3）证CG∥BD知∠GCB＝∠CBD＝∠CAD，由CE＝BE＝BC＝AC知tan∠GCB＝tan∠CAD＝，据此设GH＝BH＝a，则CH＝2a、BC＝3a、BE＝a、EH＝a，在Rt△EGH中利用勾股定理可得a的值，即可知CE＝3，再根据tan∠GCB＝，可设EF＝x、CF＝2x，在Rt△CEF中利用勾股定理求得x的值即可得出答案．

（1）如图1，连接AD，

∵AB是⊙O的直径，

∴∠ACB＝∠ADB＝90°，

∵点C是的中点，

∴AC＝BC，

则△ABC是等腰直角三角形，

∴∠CAB＝∠CBA＝45°，

设∠CBK＝∠DAC＝α，

则∠DAB＝∠DCB＝45°﹣α，∠K＝90°﹣α，

∴∠AKB﹣∠BCD＝45°；

（2）如图1，过点C作CH⊥AD，

∵∠CDH＝∠CBA＝45°，

∴CD＝CH，

∵CD＝DB，

∴CH＝DB，

∵∠CEH＝∠BED、∠CHE＝∠BDE＝90°，

∴△EBD≌△EHC（AAS），

∴CE＝BE＝BC，

∵∠CAE＝∠CBK、∠ACE＝∠BCK、AC＝BC，

∴△ACE≌△BCK（ASA），

∴CK＝CE＝BE＝BC，

即BC＝2CK；

（3）如图2，过点G作GH⊥BC于点H，则∠GHC＝90°，

∵AB是直径，

∴∠ADB＝90°，

∵CG⊥AD于点F，

∴∠CFE＝∠ADB＝90°，

∴CG∥BD，

∴∠GCB＝∠CBD＝∠CAD，

∵∠ACE＝90°，CE＝BE＝BC＝AC，

∴tan∠GCB＝tan∠CAD＝，

∴，

∵∠ABC＝45°，∠GHB＝90°，

∴GH＝BH，

设GH＝BH＝a，则CH＝2a、BC＝3a，

∴BE＝a，EH＝a，

在Rt△EGH中，( a）2+a2＝52，

解得：a＝2（负值舍去），

∴CE＝3，

∵tan∠GCB＝ ，

∴，

设EF＝x、CF＝2x，

∴x2+（2x）2＝（3）2，

解得：x＝3（负值舍去），

∴CF＝6，

∵∠CDA＝∠CBA＝45°，

∴CD＝6．