题目内容
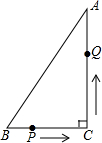 如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当t为何值时,P、Q两点的距离为5 cm?
cm?
(2)当t为何值时,△PCQ的面积为15cm2?
(3)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
解:(1)∵在Rt△ABC中,AC=24cm,BC=7cm,
∴AB=25cm,
设经过ts后,P、Q两点的距离为5 cm,
cm,
ts后,PC=7-2t cm,CQ=5t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7-2t)2+(5t)2=(5 )2;
)2;
解得t=1或t=-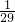 (不合题意舍去);
(不合题意舍去);
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ= =
= ×(7-2t)×5t=15
×(7-2t)×5t=15
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2
(3)设经过ts后,△PCQ的面积最大,则此时四边形BPQA的面积最小,
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ= ×PC×CQ=
×PC×CQ= ×(7-2t)×5t=
×(7-2t)×5t= ×(-2t2+7t)
×(-2t2+7t)
当t=- 时,即t=
时,即t= =1.75s时,△PCQ的面积最大,
=1.75s时,△PCQ的面积最大,
即S△PCQ= ×PC×CQ=
×PC×CQ= ×(7-2×1.75)×5×1.752=
×(7-2×1.75)×5×1.752=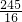 (cm2),
(cm2),
∴四边形BPQA的面积最小值为:S△ABC-S△PCQ最大= ×7×24-
×7×24-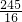 =
=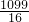 (cm2),
(cm2),
当点P运动1.75秒时,四边形BPQA的面积最小为: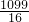 cm2.
cm2.
分析:(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过1s后,P、Q两点的距离为5 cm2
cm2
(2)根据三角形的面积公式S△PCQ= ×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2
×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2
(3)根据三角形的面积公式S△PCQ= ×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
点评:本题主要考查了勾股定理和三角形面积公式的求法以及二次函数的应用,是各地中考的热点,属于中档题.
∴AB=25cm,
设经过ts后,P、Q两点的距离为5
 cm,
cm,ts后,PC=7-2t cm,CQ=5t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7-2t)2+(5t)2=(5
 )2;
)2;解得t=1或t=-
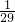 (不合题意舍去);
(不合题意舍去);(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=
 =
= ×(7-2t)×5t=15
×(7-2t)×5t=15解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2
(3)设经过ts后,△PCQ的面积最大,则此时四边形BPQA的面积最小,
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=
 ×PC×CQ=
×PC×CQ= ×(7-2t)×5t=
×(7-2t)×5t= ×(-2t2+7t)
×(-2t2+7t)当t=-
 时,即t=
时,即t= =1.75s时,△PCQ的面积最大,
=1.75s时,△PCQ的面积最大,即S△PCQ=
 ×PC×CQ=
×PC×CQ= ×(7-2×1.75)×5×1.752=
×(7-2×1.75)×5×1.752=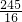 (cm2),
(cm2),∴四边形BPQA的面积最小值为:S△ABC-S△PCQ最大=
 ×7×24-
×7×24-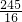 =
=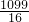 (cm2),
(cm2),当点P运动1.75秒时,四边形BPQA的面积最小为:
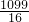 cm2.
cm2.分析:(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过1s后,P、Q两点的距离为5
 cm2
cm2(2)根据三角形的面积公式S△PCQ=
 ×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2
×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2(3)根据三角形的面积公式S△PCQ=
 ×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.点评:本题主要考查了勾股定理和三角形面积公式的求法以及二次函数的应用,是各地中考的热点,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).