题目内容
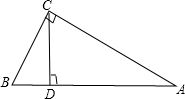
△ABC中,∠ACB=90°,高CD= ,AC=
,AC= ,求∠BCD的正弦值、余弦值、正切值.
,求∠BCD的正弦值、余弦值、正切值.
解:已知如图:
∵∠ACB=90°,
CD⊥AB,
∴∠BCD=∠A,
在Rt△ACD中,
AD2=AC2-CD2=6-2=4,
AD=2,
∴sinA= =
=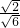 =
= ,
,
cosA= =
= =
= ,
,
tanA= =
= ,
,
∵∠BCD=∠A,
所以∠BCD的正弦值、余弦值、正切值分别为: ,
, ,
, .
.
分析:由已知可得∠BCD=∠A,由勾股定理求出AD,再根据三角函数定义求出∠A的正弦值、余弦值、正切值即∠BCD的正弦值、余弦值、正切值.
点评:此题考查的知识点是解直角三角形的应用,关键是把求∠BCD的正弦值、余弦值、正切值转化为求∠A的正弦值、余弦值、正切值.
∵∠ACB=90°,
CD⊥AB,
∴∠BCD=∠A,
在Rt△ACD中,
AD2=AC2-CD2=6-2=4,
AD=2,
∴sinA=
 =
=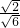 =
= ,
,cosA=
 =
= =
= ,
,tanA=
 =
= ,
,∵∠BCD=∠A,
所以∠BCD的正弦值、余弦值、正切值分别为:
 ,
, ,
, .
.
分析:由已知可得∠BCD=∠A,由勾股定理求出AD,再根据三角函数定义求出∠A的正弦值、余弦值、正切值即∠BCD的正弦值、余弦值、正切值.
点评:此题考查的知识点是解直角三角形的应用,关键是把求∠BCD的正弦值、余弦值、正切值转化为求∠A的正弦值、余弦值、正切值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 已知:如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB上的一点,且CD=AC=3,AB=4,求cosB,sin∠ADC及
已知:如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB上的一点,且CD=AC=3,AB=4,求cosB,sin∠ADC及 如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=20,AC=10,则图中等于30°的角的个数为( )
如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=20,AC=10,则图中等于30°的角的个数为( ) 如图,在△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB等腰三角形,则符合条件的点P共有
如图,在△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB等腰三角形,则符合条件的点P共有 如图,在Rt△ABC中,∠ACB=90°,⊙O为△ABC的外接圆,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.若⊙P与⊙O相切,则t的值是( )
如图,在Rt△ABC中,∠ACB=90°,⊙O为△ABC的外接圆,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.若⊙P与⊙O相切,则t的值是( ) 如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.