题目内容
 已知:如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.
已知:如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.求证:△ABC≌△DEF.
分析:由AC∥DF,则∠ACE=∠DFB,所以,∠ACB=∠DFE,又BF=EC,则BF-CF=EC-CF=EF,即BC=EF,即可证明△ABC≌△DEF(AAS).
解答:证明:∵AC∥DF,
∴∠ACE=∠DFB,
∴∠ACB=∠DFE,
又∵BF=EC,
∴BF-CF=EC-CF,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF.
∴∠ACE=∠DFB,
∴∠ACB=∠DFE,
又∵BF=EC,
∴BF-CF=EC-CF,
∴BC=EF,
在△ABC与△DEF中,
|
∴△ABC≌△DEF.
点评:本题主要考查了全等三角形的判定,熟练掌握两直线平行,内错角相等,及等式的性质,是推导出两三角形全等的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
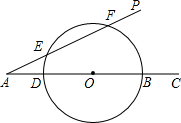 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.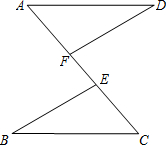 13、已知:如图,E、F在AC上,AD∥CB且AD=CB,∠D=∠B.
13、已知:如图,E、F在AC上,AD∥CB且AD=CB,∠D=∠B.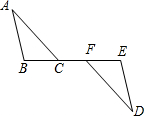 已知:如图,C、F在BE上,∠A=∠D,AB∥DE,AB=DE.
已知:如图,C、F在BE上,∠A=∠D,AB∥DE,AB=DE. 22、已知:如图,D、E在BC上,AB=AC,AD=AE.试说明线段BD与CE相等的理由.
22、已知:如图,D、E在BC上,AB=AC,AD=AE.试说明线段BD与CE相等的理由.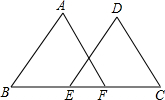 已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD
已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD