题目内容
【题目】已知,如图![]() ,且
,且![]() ,
,![]() .其中
.其中![]() 、
、![]() 、
、![]() 共线且
共线且![]() 交
交![]() 于
于![]() .
.
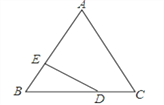
(1)如图1,若![]() 为
为![]() 的中点,且
的中点,且![]() ,求
,求![]() 的长.
的长.
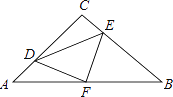
(2)如图2,若![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]()

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)只要证明△DAC≌△EAB,推出CD=EB,∠ACD=∠ABE,由∠CFD=∠AFB,推出∠CDF=∠FAB=90°,再求出CD、BD,利用勾股定理求出BC即可解决问题.
(2)如图2中,延长AE交BC于J.想办法证明CA=CJ,BJ=BG即可解决问题.
(1)如图1中,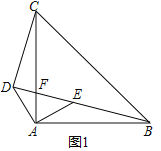
∵△ABC和△ADE均为等腰直角三角形,
∴∠BAC=∠EAD=90°,AB=AC,AE=AD=1,
∴∠EAB=∠DAC,
∴△DAC≌△EAB,
∴CD=EB=![]() ,∠ACD=∠ABE,
,∠ACD=∠ABE,
∵∠CFD=∠AFB,
∴∠CDF=∠FAB=90°,
∵DE=EB=CD=![]() ,
,
∴BC=![]() ,
,
∴AB=AC=![]() .
.
(2)如图2中,延长AE交BC于J.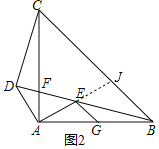
∵DE=![]() BE,DE=
BE,DE=![]() AE,
AE,
∴AE=EB,
∴∠EAB=∠EBA,
∵∠DEA=45°=∠EAB+∠EBA,
∵EF=BE,∠BAF=90°,
∴∠EAB=∠EBA=∠EBC=22.5°,
∴∠CAE=67.5°,
∴∠CJA=180°-∠CAJ-∠ACJ=67.5°,
∴∠CAJ=∠CJA,
∴CA=CJ=CB,
∵EG⊥AE,
∴∠AEG=∠GEJ=90°,
∴∠AGE=90°-22.5°=67.5°,
∵∠AGE=∠EBG+∠GEB,
∴∠BEG=45°=∠BEJ,
∵BE=BE,∠EBJ=∠EBG,
∴△EBJ≌△EBG(ASA),
∴BG=BJ,
∴BC=CJ+BJ=AB+BG.

练习册系列答案
相关题目