题目内容
【题目】如图,四边形![]() 是
是![]() 的内接矩形,如果
的内接矩形,如果![]() 的高线
的高线![]() 长
长![]()
![]() ,底边
,底边![]() 长
长![]()
![]() ,设
,设![]()
![]() ,
,![]()
![]() ,
,
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时, 四边形
为何值时, 四边形![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
【答案】(1)y=8-![]() x;(2)当x=5时,四边形DEFG面积最大,最大面积是20.
x;(2)当x=5时,四边形DEFG面积最大,最大面积是20.
【解析】
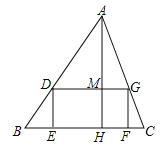
试题分析:(1)设DE=y,则MH=y,AM=AH-MH=8-y,因为DG∥BC,可证△ADG∽△ABC,根据相似三角形对应边上高的比等于相似比,建立等式;
(2)设四边形DEFG的面积为S,则S=DE×DG=xy=x(8-![]() x),运用二次函数性质解决问题.
x),运用二次函数性质解决问题.
试题解析:(1)设AH与DG交于点M,则AM=AH-MH=8-y,
∵DG∥BC,∴△ADG∽△ABC,
∴![]() ,即
,即![]() ,
,
整理,得y=8-![]() x;
x;
(2)设四边形DEFG的面积为S,则S=DE×DG=xy=x(8-![]() x)=-
x)=-![]() x2+8x,
x2+8x,
当x=-![]() =5时,S=-
=5时,S=-![]() ×25+8×5=20,
×25+8×5=20,
所以当x=5时,四边形DEFG面积最大,最大面积是20.

练习册系列答案
相关题目