题目内容
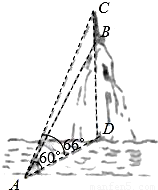
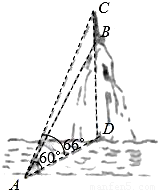
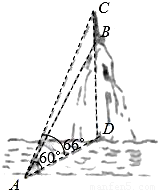
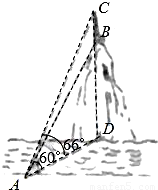
某数学兴趣小组在学习了《锐角三角函数》以后，开展测量物体高度的实践活动，他们在河边的一点A测得河对岸小山顶上一座铁塔的塔顶C的仰角为66°、塔底B的仰角为60°，已知铁塔的高度BC为20m（如图），你能根据以上数据求出小山的高BD吗？若不能，请说明理由；若能，请求出小山的高BD．（精确到0.1m）（参考数据：sin66°≈0.9135，cos66°≈0.4067，tan66°≈2.2460）
分析：在Rt△ABD中，知道∠BAD=60°，在Rt△ACD中知道∠CAD=66°，AD是Rt△ABD和Rt△ACD的公共边，求BD的长，而DC=BD+BC=BD+20，设BD为x，用AD的长度作为相等关系，列方程即可求出BD．
解答：解：能求出小山的高．
设小山的高BD为xm，
在Rt△ABD中，
=tan∠BAD=tan60°，AD=
，
同理，在Rt△ACD中得AD=
=
，
∴
=
，
解得：x=
=
≈67.4，
答：小山的高BD约为67.4m．
设小山的高BD为xm，
在Rt△ABD中，
| BD |
| AD |
| x |
| tan60° |
同理，在Rt△ACD中得AD=
| CD |
| tan66° |
| x+20 |
| tan66° |
∴
| x |
| tan60° |
| x+20 |
| tan66° |
解得：x=
| 20tan60° |
| tan66°-tan60° |
20
| ||
tan66°-
|
答：小山的高BD约为67.4m．
点评：主要考查了从实际问题中抽象出几何图形的能力，把实际问题转化为数学问题来解决，本题主要运用了解直角三角形中的三角函数，所以要掌握一个角所对应正弦，余弦，正切值的表示方法，并会用三角函数值求边长．
练习册系列答案
相关题目
