题目内容

如图所示，矩形ABCD的面积为10 cm²，它的两条对角线交于点O₁，以AB，AO₁为邻边作平行四边形ABC₁O₁，平行四边形ABC₁O₁的对角线交于点O₂，同样以AB，AO₂为邻边作平行四边形ABC₂O₂，…，依此类推，则平行四边形ABC₅O₅的面积为

A.
1cm²
B.
2cm²
C.
$数学公式$ cm²
D.
$数学公式$ cm²

D
分析：由规律发现边长为原来的 $\text{[math]}$ ，面积为原来的 $\text{[math]}$ ，然后根据规律求解．
解答：

解：根据题意分析可得：
∵四边形ABCD是矩形，
∴O₁A=O₁C，
∵四边形ABC₁0₁是平行四边形，
∴O₁C₁∥AB，
∴BE= $\text{[math]}$ BC，
∵S_矩形ABCD=AB•BC，S_?ABC1O1=AB•BE= $\text{[math]}$ AB•BC，
∴面积为原来的 $\text{[math]}$ ；
同理：每个平行四边形均为上一个面积的 $\text{[math]}$ ，
故平行四边形ABC₅O₅的面积为10×（ $\text{[math]}$ ）⁵= $\text{[math]}$ cm²．
故选D．
点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．

练习册系列答案

通成学典课时作业本系列答案

教学练新同步练习系列答案

黄冈小状元作业本系列答案

课时达标练与测系列答案

课前课后同步练习系列答案

经纶学典课时作业系列答案

课堂小作业系列答案

黄冈小状元口算速算练习册系列答案

成功训练计划系列答案

倍速训练法直通中考考点系列答案

相关题目

如图①，在平面直角坐标系中，已知△ABC是等边三角形，点B的坐标为（12，0），动点P在线段AB上从点A向点B以每秒

个单位的速度运动，设运动时间为t秒．以点P为顶点，作等边△PMN，点M，N在x轴上．
（1）当t为何值时，点M与点O重合；
（2）求点P坐标和等边△PMN的边长（用t的代数式表示）；
（3）如果取OB的中点D，以OD为边在△AOB内部作如图②所示的矩形ODEF，点E在线段AB上．设等边△PMN和矩形ODEF重叠部分的面积为S，请求出当0≤t≤2秒时S与t的函数关系式，并求出S的最大值．

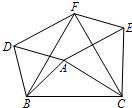18、如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE、等边△BCF．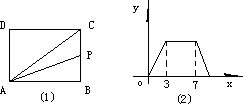
（1）求证：四边形DAEF是平行四边形；
（2）探究下列问题：（只填满足的条件，不需证明）
①当△ABC满足

条件时，四边形DAEF是矩形；
②当△ABC满足

条件时，四边形DAEF是菱形；
③当△ABC满足

条件时，以D、A、E、F为顶点的四边形不存在．

17、如图①在矩形ABCD中，动点P从点B出发，沿着BC、CD、DA运动到点A停止，设点P运动的路程为x，△ABP的面积为y，如果y与x的函数图象如图②所示，则△ABC的周长为

如图，已知△ABC是等边三角形，点O为是AC的中点，OB=12，动点P在线段AB上从点A向点B以每秒

个单位的速度运动，设运动时间为t秒．以点P为顶点，作等边△PMN，点M，N在直线OB上，取OB的中点D，以OD为

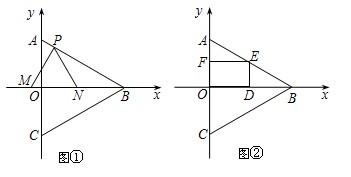
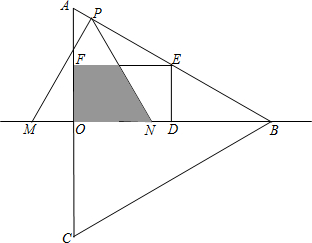边在△AOB内部作如图所示的矩形ODEF，点E在线段AB上．
（1）求当等边△PMN的顶点M运动到与点O重合时t的值；
（2）求等边△PMN的边长（用t的代数式表示）；
（3）设等边△PMN和矩形ODE F重叠部分的面积为S，请求你直接写出当0≤t≤2秒时S与t的函数关系式，并写出对应的自变量t的取值范围；
（4）点P在运动过程中，是否存在点M，使得△EFM是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．

（2012•邵阳）如图所示，在△ABC中，AB=AC，∠A＜90°，边BC、CA、AB的中点分别是D、E、F，则四边形AFDE是（　　）