题目内容
如图，△AOD关于直线l进行轴对称变换后得到△BOC，下列说法中不正确的是
- A.∠DAO=∠CBO，∠ADO=∠BCO
- B.直线l垂直平分AB、CD
- C.△AOD和△BOC均是等腰三角形
- D.AD=BC，OD=OC
C
分析：根据轴对称的性质易得∠DAO=∠CBO，∠ADO=∠BCO，直线l垂直平分AB、CD，AD=BC，OD=OC．
解答：∵△AOD关于直线l进行轴对称变换后得到△BOC，
∴∠DAO=∠CBO，∠ADO=∠BCO，直线l垂直平分AB、CD，AD=BC，OD=OC．
∵题设中没有给定△AOD为等腰三角形，
∴△BOC的形状不能确定，
所以A、B、D选项的说法正确；C选项的说法错误．
故选C．
点评：本题考查了轴对称的性质：关于某直线对称的两图象全等，即对应角相等，对应线段相等；对应点的连线段被对称轴垂直平分．
分析：根据轴对称的性质易得∠DAO=∠CBO，∠ADO=∠BCO，直线l垂直平分AB、CD，AD=BC，OD=OC．
解答：∵△AOD关于直线l进行轴对称变换后得到△BOC，
∴∠DAO=∠CBO，∠ADO=∠BCO，直线l垂直平分AB、CD，AD=BC，OD=OC．
∵题设中没有给定△AOD为等腰三角形，
∴△BOC的形状不能确定，
所以A、B、D选项的说法正确；C选项的说法错误．
故选C．
点评：本题考查了轴对称的性质：关于某直线对称的两图象全等，即对应角相等，对应线段相等；对应点的连线段被对称轴垂直平分．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
21、画出如图中△ABC关于直线MN的对称三角形．
如图，△AOD关于直线l进行轴对称变换后得到△BOC，下列说法中不正确的是（ ）
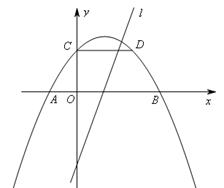
关于直线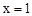
对称，与坐标轴交于A、B、C三点，且AB=4，点D
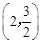在抛物线上，直线
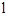是一次函数
的图象，点O是坐标原点.
