题目内容
【题目】如图，抛物线与
轴交于点
和点
，与
轴交于点
，其对称轴
为
，
为抛物线上第二象限的一个动点．
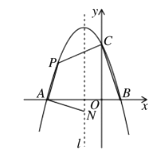
（1）求抛物线的解析式并写出其顶点坐标；
（2）当点在运动过程中，求四边形
面积最大时的值及此时点的坐标．
【答案】（1）
，(－1，4)；（2）
，P(
，
)
【解析】
（1）根据题意将已知点的坐标代入已知的抛物线的解析式，利用待定系数法确定抛物线的解析式并写出其顶点坐标即可；
（2）根据题意设P点的坐标为（t，
）(－3＜t＜0)，并用分割法将四边形的面积S四边形BCPA= S△OBC＋S△OAP＋S△OPC，得到二次函数运用配方法求得最值即可．
解：（1）∵该抛物线过点C(0，3)，
∴可设该抛物线的解析式为
，
∵与x轴交于点A和点B（1，0），其对称轴l为x=－1，
∴
∴
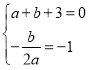
∴此抛物线的解析式为，
其顶点坐标为（－1，4）；
（2）如图：
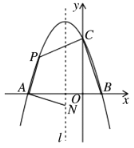
可知A（－3，0），
∴OA＝3，OB＝1，OC＝3
设P点的坐标为（t，）(－3＜t＜0)
∴S四边形BCPA＝S△OBC＋S△OAP＋S△OPC
＝
×OB×OC＋×OA×yP＋×xC×OC
＝×1×3＋×3×()＋×|t|×3
＝
＝
＝
∴当t＝时，四边形PABC的面积有最大值
∴P（，）.
练习册系列答案
相关题目
