题目内容
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD. 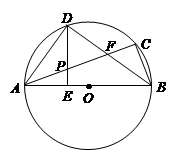
【小题1】求证:∠DAC =∠DBA;
【小题2】求证: 是线段AF的中点
是线段AF的中点
【小题3】若⊙O 的半径为5,AF =  ,求tan∠ABF的值.
,求tan∠ABF的值.
【小题1】∵BD平分∠CBA,∴∠CBD=∠DBA
∵∠DAC与∠CBD都是弧CD所对的圆周角,∴ ∠DAC=∠CBD
∠DAC=∠CBD
∴ ∠DAC =∠DBA (2分)
∠DAC =∠DBA (2分)
【小题2】∵AB为直径,∴∠ADB=90°
又∵DE⊥AB于点E,∴∠DEB=90° ∴∠ADE +∠EDB=∠ABD +∠EDB=90°
∴∠ADE=∠ABD=∠DAP
∴PD=PA
又∵∠DFA +∠DAC=∠ADE +∠PD F=90°且∠ADE=∠DAC
∴∠PDF=∠PFD
∴PD=PF ∴PA= PF 即P是线段AF的中点 (3分)
【小题3】∵∠DAF =∠DBA,∠ADB=∠FDA=90°∴△FDA ∽△ADB
∴
∴在Rt△ABD 中,tan∠ABD= ,即tan∠ABF=
,即tan∠ABF= (3分)
(3分)
解析

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

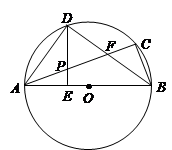
 是线段AF的中点
是线段AF的中点 ,求tan∠ABF的值.
,求tan∠ABF的值.
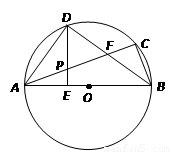
 是线段AF的中点
是线段AF的中点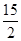 ,求tan∠ABF的值.
,求tan∠ABF的值.