题目内容
若不等式组 (x为未知数)无解,则二次函数的图象y=ax2-4x+1与x轴的交点
(x为未知数)无解,则二次函数的图象y=ax2-4x+1与x轴的交点
- A.没有交点
- B.一个交点
- C.两个交点
- D.不能确定
C
分析:先根据不等式组 (x为未知数)无解求出a的取值范围,再根据y=ax2-4x+1中a的取值范围判断出△的符号即可.
(x为未知数)无解求出a的取值范围,再根据y=ax2-4x+1中a的取值范围判断出△的符号即可.
解答:∵不等式组 (x为未知数)无解,
(x为未知数)无解,
∴a≤3,
∴4a≤12,-4a≥-12,
∴16-4a≥4,
∵△=(-4)2-4a×1=16-4a≥4,
∴二次函数的图象y=ax2-4x+1与x轴有两个交点.
故选C.
点评:本题考查的是抛物线与x轴的交点,根据题意判断出16-4a的取值范围是解答此题的关键.
分析:先根据不等式组
 (x为未知数)无解求出a的取值范围,再根据y=ax2-4x+1中a的取值范围判断出△的符号即可.
(x为未知数)无解求出a的取值范围,再根据y=ax2-4x+1中a的取值范围判断出△的符号即可.解答:∵不等式组
 (x为未知数)无解,
(x为未知数)无解,∴a≤3,
∴4a≤12,-4a≥-12,
∴16-4a≥4,
∵△=(-4)2-4a×1=16-4a≥4,
∴二次函数的图象y=ax2-4x+1与x轴有两个交点.
故选C.
点评:本题考查的是抛物线与x轴的交点,根据题意判断出16-4a的取值范围是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
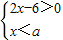 (x为未知数)无解,则二次函数的图象y=ax2-4x+1与x轴的交点( )
(x为未知数)无解,则二次函数的图象y=ax2-4x+1与x轴的交点( ) (x为未知数)无解,则函数y=(3-a)x2-x+
(x为未知数)无解,则函数y=(3-a)x2-x+ 的图象与x轴( )
的图象与x轴( )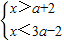 (x为未知数)无解,则函数y=(3-a)x2-x+
(x为未知数)无解,则函数y=(3-a)x2-x+ 的图象与x轴( )
的图象与x轴( ) (x为未知数)无解,则函数y=(3-a)x2-x+
(x为未知数)无解,则函数y=(3-a)x2-x+ 的图象与x轴( )
的图象与x轴( ) (x为未知数)无解,则函数y=(3-a)x2-x+
(x为未知数)无解,则函数y=(3-a)x2-x+ 的图象与x轴( )
的图象与x轴( )