题目内容
证明: ≤
≤ +
+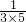 +…+
+…+ <
< (n为正整数).
(n为正整数).
证明: +
+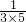 +…+
+…+ =
= (1-
(1- )+
)+ (
( -
- )+…+
)+…+ (
( -
- )
)
= (1-
(1- +
+ -
- +…+
+…+ -
- )
)
= (1-
(1- )
)
= •
•
= ,
,
∵ ≤
≤ <
<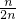 ,(n为正整数,n=1时
,(n为正整数,n=1时 最小),
最小),
∴ ≤
≤ <
< ,
,
∴ ≤
≤ +
+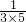 +…+
+…+ <
< (n为正整数).
(n为正整数).
分析:利用 =
= (
( -
- )把
)把 +
+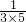 +…+
+…+ (n为正整数)的每个分数进行转化得到
(n为正整数)的每个分数进行转化得到 +
+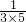 +…+
+…+ =
= (1-
(1- )+
)+ (
( -
- )+…+
)+…+ (
( -
- )=
)= (1-
(1- +
+ -
- +…+
+…+ -
- ),然后进行括号内的加减运算,最后得到
),然后进行括号内的加减运算,最后得到 ,n为正整数,当n=1时
,n为正整数,当n=1时 最小;并且
最小;并且 <
<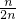 =
= ,即可得到结论.
,即可得到结论.
点评:本题考查了有理数的混合运算:当n为正整数,分数 可化为分数
可化为分数 与
与 分数的差的
分数的差的 .
.
 +
+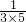 +…+
+…+ =
= (1-
(1- )+
)+ (
( -
- )+…+
)+…+ (
( -
- )
)=
 (1-
(1- +
+ -
- +…+
+…+ -
- )
)=
 (1-
(1- )
)=
 •
•
=
 ,
,∵
 ≤
≤ <
<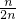 ,(n为正整数,n=1时
,(n为正整数,n=1时 最小),
最小),∴
 ≤
≤ <
< ,
,∴
 ≤
≤ +
+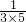 +…+
+…+ <
< (n为正整数).
(n为正整数).分析:利用
 =
= (
( -
- )把
)把 +
+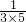 +…+
+…+ (n为正整数)的每个分数进行转化得到
(n为正整数)的每个分数进行转化得到 +
+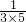 +…+
+…+ =
= (1-
(1- )+
)+ (
( -
- )+…+
)+…+ (
( -
- )=
)= (1-
(1- +
+ -
- +…+
+…+ -
- ),然后进行括号内的加减运算,最后得到
),然后进行括号内的加减运算,最后得到 ,n为正整数,当n=1时
,n为正整数,当n=1时 最小;并且
最小;并且 <
<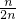 =
= ,即可得到结论.
,即可得到结论.点评:本题考查了有理数的混合运算:当n为正整数,分数
 可化为分数
可化为分数 与
与 分数的差的
分数的差的 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 22、如图,已知:点B,F,C,D在同一直线上,且FB=CD,AB∥ED,AC∥FE,请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.
22、如图,已知:点B,F,C,D在同一直线上,且FB=CD,AB∥ED,AC∥FE,请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.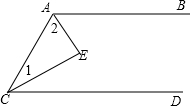 如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E为多少?
如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E为多少? 为半径作⊙O.
为半径作⊙O. 20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C
20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C